قانون كيرشوف الأول للتيار
اكتشف عالم الفيزياء الألماني جوستاف روبرت كيرشوف (بالإنجليزية: Gustav Robert Kirchhoff) قوانين كيرشوف التي تسمح بحساب التيارات وشدّتها ومقاومات الشبكات الكهربائية، والتي أعلن عنها لأول مرّة في عام 1845م.[١] وفيما يأتي تفسير لقانون كيرشوف الأول للتيار:
نص قانون كيرشوف الأول وشرحه
ينصّ قانون كيرشوف الأول للتيار (بالإنجليزية: Kirchhoff's Current Law) على أنّ التيار المتدفّق إلى عقدة أو تقاطع أسلاك في دارة يجب أن يكون مساويًا للتيار الخارج من ذلك التقاطع، ويكون ذلك نتيجةً للحفاظ على الشحنة، فمن أهم المفاهيم الأساسية في الفيزياء أنّ الشحنة ستبقى دائمًا محفوظة في الدارة المغلقة، ونظرًا لأنّ التيار هو معدّل تدفّق الشحنة، فإنّ التيار الذي يتدفّق إلى نقطة ما يجب أن يكون هو ذاته التيار الخارج من تلك النقطة.[٢]
كما وتنصّ صيغة قانون كيرشوف الأول على أنّ مجموع التيارات في أي عقدة (الداخلة والخارجة) في الدارة الكهربائية يساوي دائمًا صفرًا.[٣]
صيغة قانون كيرشوف الأول
يصاغ قانون كيرشوف الأول رياضيًا بحسب عدد التيارات على النحو الآتي:[٣]
شدة التيار الأول + شدة التيار الثاني + شدّة التيار الثالث + ...= 0
وبالرموز:
ت1 + ت2 + ت3 + ... = 0
وبالإنجليزية:
Current1 + Current2 + Current3 + ... =0
وبالرموز الإنجليزية:
I1 + I2 + I3+ ... = 0
إذ إنّ:
- ت (I) : التيار الأول، بوحدة الأمبير (A).
ويجب الانتباه إلى أنّ التيارات التي تتدفق نحو التقاطع تكون موجبة، بينما التي تخرج منها تكون سالبة.[٣]
تدريبات على قانون كيرشوف الأول
وفيما يأتي بعض الأمثلة على قانون كيرشوف الأول:
إيجاد قيمة تيار مجهول
مجموعة من التيارات المتدفّقة تلتقي في عقدة واحدة، بحيث تكون شدّة التيار الأول المتدفّق باتجاه العقدة 0.2 أمبير، وشدّة التيار الثاني الخارج من العقدة 0.4 أمبير، وشدّة التيار الثالث المتدفّق باتجاه العقدة 0.5 أمبير، جد قيمة التيار الرابع الخارج منها.
الحل:
- المعطيات: ت1 = 0.2 ، ت2 = 0.4 ، ت3 = 0.5.
- يتم جمع التيار المتدفّق وطرح التيار الخارج، وبالتالي وبتطبيق قانون كيرشوف الأول: ت1 + ت2 + ت3 + ... = 0
- تعوض القيم في القانون؛ 0.2 - 0.4 + 0.5 - ت4 = 0
- ومنه؛ 0.7 - ت4 = 0
- وبالتالي فإن قيمة التيار الرابع (ت4) = -0.7 أمبير (الإشارة السالبة تعبر عن أن التيار خارج من العقدة).
إيجاد قيمة تياريْن مجهولين
يتدفق التيار الأول (تيار داخل) بشدّة تساوي 3 أمبير، ويتفرّع إلى تيار ثاني وثالث (تيارات خارجة)، ثمّ يلتقي التيارين الثاني والثالث معًا في تقاطع آخر ليخرج تيار رابع، فإذا كانت شدّة التيار الثاني 2 أمبير، جد قيمة التيار الثالث، وقيمة التيار الرابع.
الحل:
- لإيجاد قيمة التيار الثالث:
- المعطيات: ت1 = 3 أمبير، ت2 = 2 أمبير، ت3 = ؟
- يُطبّق قانون كيرشوف الأول: ت1 + ت2 + ت3 + ... = 0
- وبالتالي: 3 - 2 - ت3 = 0
- ومنها: 1 - ت3 = 0.
- إذًا؛ التيار الثالث (ت3)= 1 أمبير.
- لإيجاد قيمة التيار الرابع؛ باعتباره تيارًا خارجًا موحدًا للتياريْن الثاني والثالث الداخلين.
- المعطيات: ت2 = 2 أمبير، ت3 = 1 أمبير، ت4 = ؟
- يُطبق قانون كيرشوف الأول: ت1 + ت2 + ت3 + ... = 0
- 2 + 1 - ت4 = 0، ومنها:
- 3 - ت4 = 0.
- إذًا؛ التيار الرابع (ت4)= 3 أمبير.
إيجاد قيمة تيار من قيمة التيار الكلي
إذا كانت قيمة التيار الكلي في العقدة هي 7 أمبير، تتفرّع إلى تياريْن، قيمة التيار الأول الذي يتفرّع ويخرج منها 3 أمبير، فما قيمة التيار الثاني الذي يخرج منها أيضًا؟
الحل:
- المعطيات: التيار الكلي ت= 7 أمبير، ت1 = 3 أمبير، ت2 = ؟؟
- وبتطبيق قانون كيرشوف الأول للتيار فإنّ التيار الكلي= مجموع التيارات الأخرى، تكون الصيغة:
- 7 = 3 + ت2، ومنها:
- ت2 = 7 - 3
- ت2 = 4 أمبير.
ينص قانون كيرشوف الأول على أنّ مجموع التيار المتدفق إلى عقدة أو تقاطع يساوي التيار الخارج من ذلك التقاطع، ويُعبّر عن ذلك بأنّ التيار الكلي الداخل إلى الدارة يساوي مجموع التيارات الخارجة منها، وبالتالي يكون مجموع التيارات جميعا يساوي صفر، وفقًا للصيغة الرياضية: ت1 + ت2 + ت3 + ... = 0.
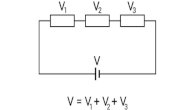
قانون كيرشوف الثاني للجهد
أُعلن عن قانون كيرشوف الثاني أو ما يُسمى بقانون الجهد بعد القانون الأول للتيار أي في عام 1847م.[٤] وفيما يأتي تفصيل لهذا القانون:
نص قانون كيرشوف الثاني وشرحه
ينصّ قانون كيرشوف الثاني للجهد (بالإنجليزية: Kirchhoff’s Voltage Law) على أنّ مجموع فرق الجهد عبر دارة كهربائية مغلقة يساوي صفرًا، أو أنّ القوة الكهربائية الدافعة والمؤثّرة على العُقد في دارة مغلقة مساوية لمجموع فرق الجهد الموجود عبر هذه الدارة المغلقة، وعادةً ما يُتبع هذا القانون بقانون حفظ الطاقة، وبالتالي يمكن استنتاج ما يأتي:[٥]
- تكون كمية الشحنة المكتسبة في دارة مغلقة مساوية لكمية الطاقة التي تفقدها، ويعود سبب هذا الفقدان إلى المقاومات المتّصلة في هذه الدارة المغلقة.
- يجب أن يكون مجموع فرق الجهد عبر الدارة المغلقة صفرًا.
صيغة قانون كيرشوف الثاني
وفقًا لنص القانون، تكون صيغة قانون كيرشوف الثاني للجهد كالآتي:[٦]
الجهد الكهربائي1 + الجهد الكهربائي2 + الكهربائي3 + ...= 0
وبالرموز:
جـ1 + جـ2 + جـ3 + ...= 0
وبالإنجليزية:
voltage1 + voltage2 + voltage3 + .... = 0
وبالرموز:
ΣV = 0
أي أن:
V1+V2+V3+ ... = 0
إذ إنّ:
- جـ (V): هو الجهد في الحلقة المغلقة في الدارة، ويقاس بوحدة الفولت (Volt).
وهذا يعني بأنّ المجموع الجبري لفروق الجهد -على اختلافها- حول الحلقة المغلقة في الدارة الكهربائية مساويًا للصفر؛ لذا يجب مراعاة القطبية وأماكن انخفاض الجهد حول الحلقة، فعند انخفاض الجهد يجب طرحه من المعادلة المذكورة (إشارته سالبة لا موجبة).[٦]
ولمعرفة قيمة الجهد في دارة تحتوي على مقاومة واحدة أو مجموعة مقاومات موصولة على التوالي، يمكن استخدام قانون أوم (Ohm's Law) والذي ينصّ على:[٧]
الجهد = شدة التيار × المقاومة
وبالرموز:
جـ = ت × م
وبالإنجليزية:
Voltage= Current × Resistance
وبالرموز الإنجليزية:
V = I × R
إذ إنّ:
- جـ (V): هو الجهد في الدارة المغلقة، ويُقاس بالفولت.
- ت (I): قيمة التيار المتدفّق في الدارة، ويقاس بالأمبير.
- م (R): المقاومة الكهربائية، والتي تقاس بالأوم (Ω).
تدريبات على قانون كيرشوف الثاني
وفيما يأتي بعض الأمثلة على قانون كيرشوف الثاني:
حساب الجهد لمقاومات متعددة
ثلاثة مقاومات ذات قيم 10 أوم و20 أوم و30 أوم، على التوالي، متصلة عبر مصدر طاقة فرق الجهد بين طرفيه يساوي 12 فولت، وشدّة التيار المار فيه 0.2 أمبير، احسب الجهد عبر كل مقاومة، وتأكد من النتيجة باستخدام قانون كيرشوف الثاني.
الحل:
- حساب الجهد عبر المقاومة الأولى: بتطبيق قانون أوم: جـ1 = ت × م1
- جـ1 = 0.2 × 10
- ومنها؛ جـ1 = 2 فولت، أي أنّ الجهد عبر المقاومة الأولى يساوي 2 فولت.
- حساب الجهد عبر المقاومة الثانية: بتطبيق قانون أوم: جـ2 = ت × م2
- جـ2 = 0.2 × 20 = 4 فولت
- جـ2= 4 فولت، أي أنّ الجهد عبر المقاومة الثانية= 4 فولت.
- حساب الجهد عبر المقاومة الثالثة: بتطبيق قانون أوم: جـ3 = ت × م3
- جـ3 = 0.2 × 30 = 6 فولت
- جـ3= 3 فولت، أي أنّ الجهد عبر المقاومة الثالثة= 6 فولت.
للتحقق من النتيجة عبر قانون كيرشوف الثاني:
- بتطبيق قانون كيرشوف الثاني: جهد البطارية + انخفاض الجهد الأول + انخفاض الجهد الثاني + انخفاض الجهد الثالث= 0، ومنها:
- 12 + (-2) + (-4) + (-6)= 0
- وبالتالي: 12 - 12 = 0، غذًا فالحل صحيح.
حساب مقدار انخفاض الجهد
في دارة مغلقة يمر تيار شدّته 0.5 أمبير، وفيها عدة مقاومات؛ الأولى 18 أوم والثانية 12 أوم، ما هو مقدار انخفاض الجهد، إذا كان جهد البطارية الأساسي 17 فولت، وتحقق من ذلك باستخدام قانون كيرشوف الثاني.
الحل:
- باستخدام قانونه أوم يحسب الجهد عبر المقاومات؛ جـ = ت × م
- الجهد عبر المقاومة الأولى: جـ1 = ت × م1
- جـ1 = 0.5 × 18
- جـ1 = 9 فولت.
- الجهد عبر المقاومة الثانية: جـ2 = ت × م2
- جـ2 = 0.5 × 16
- جـ2= 8 فولت.
- بتطبيق قانون كيرشوف الثاني: الجهد من البطارية + انخفاض الجهد الأول + انخفاض الجهد الثاني= 0، أي أنّ:
- 17 -9 - 8= 0
- وبالتالي: 17-17 = 0، وهذا صحيح.
حساب قيمة التيار وقيمة الجهد
إذا كان التيار الأول المتدفّق عبر دارة يساوي 0.3 أمبير، وقيمة المقاومة الأولى 18 أوم، والجهد 9.2 فولت، والتيار الثاني الخارج من الدارة يساوي 0.2 أمبير، والمقاومة الثانية 12 أوم، والجهد يساوي 6 فولت، فما قيمة التيار الثالث الخارج منها، وقيمة الجهد الثالث إذا كانت مقاومته 8 أوم، وجهد البطارية يساوي 16 فولت؟ وتحقق باستخدام قانون كيرشوف الثاني من صحّة الحل.
الحل:
- حساب قيمة التيار الثالث:
- باستخدام قانون كيرشوف الأول: ت1 + ت2 + ت3 = 0
- ومنها: 0.3 - 0.2 - ت3 = 0
- وبالتالي قيمة التيار الثالث (ت3) = 0.1 أمبير.
- حساب قيمة الجهد الثالث:
- باستخدام قانون أوم: جـ3 = ت3 × م3
- جـ3 = 0.1 × 8= 0.8 فولت
- بتطبيق قانون كيرشوف الثاني: الجهد من البطارية + انخفاض الجهد الأول + انخفاض الجهد الثاني + انخفاض الجهد الثالث= 0 أي:
- 16 - 9.2 - 6 - 0.8 = 0 وبالتالي:
- 16-16 = 0، إذًا فالحل صحيح.
فوائد قوانين كيرشوف
تشمل فوائد وإيجابيات قوانين كيرشوف ما يأتي:[٨]
- تحليل أي دارة كهربائية.
- حساب قيم التيارات وفرق الجهد في الدوائر المعقّدة بكل سهولة.
- تبسيط وتحليل الدوائر المعقّدة المغلقة.
ينصّ قانون كيرشوف الأول على أنّ مجموع التيارات المتدفّقة والخارجة من دارة ما تساوي صفرًا، ويصاغ قانونه رياضيًا على النحو الآتي؛ ت1 + ت2 + ت3 + ... = 0، بينما ينصّ القانون الثاني لكيرشوف على أنّ فرق الجهد في دارة مغلقة يساوي صفرًا، ويصاغ قانونه رياضيًا على النحو الآتي؛ جـ1 + جـ2 + جـ3 + ...= 0، وتفيد هذه القوانين في معرفة قيم التيارات وفرق الجهد المفقود في الدارة وتبسيط وتحليل الدارات المغلقة المعقّدة.
المراجع
- ↑ "Gustav Kirchhoff", britannica, Retrieved 6/9/2021. Edited.
- ↑ "Kirchhoff's Laws", isaacphysics, Retrieved 6/9/2021. Edited.
- ^ أ ب ت "Kirchhoff’s Laws", eepower, Retrieved 6/9/2021. Edited.
- ↑ "Kirchhoff’s Voltage Law (KVL)", www.allaboutcircuits.com, Retrieved 10/9/2021. Edited.
- ↑ "Kirchhoff’s Second Law", vedantu, Retrieved 6/9/2021. Edited.
- ^ أ ب "Kirchhoff’s Voltage Law", electronics-tutorials, Retrieved 6/9/2021. Edited.
- ↑ "Ohm's Law", byjus, Retrieved 10/9/2021. Edited.
- ↑ "Kirchhoff’s Laws of Current & Voltage – Application, Advantage, Limitation", electricalfundablog, Retrieved 6/9/2021. Edited.