محتويات

كيفية حساب زوايا المُثلث
يضم المثلث 3 زوايا ويساوي مجموع زواياه الداخليّة 180 درجة مهما اختلف نوعه، وتُشكّلان معًا زاوية مستقيمة قياسها 180 درجة؛ إذ تُوضّح المعادلة الآتية كيفية حساب زوايا المثلث:[١]
مجموع قياس زوايا المثلث الداخليّة= 180.
س+ص+ع = 180 درجة؛ حيث س، ص، ع، تُمثّل زوايا المثلث.
فإذا عُلمت قيمة زاويتين في مثلث ما، وكان قياس الزاوية الثالثة مجهولًا؛ فيُمكن حساب قياسها عن طريق طرح مجموع الزاويتين من 180 درجة، والطرق الآتية تُساهم في إيجاد قيمة زوايا المثلث بمختلف أنواعه:[١]
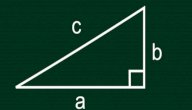
- حساب زوايا المثلث قائم الزاوية: يُعرف المثلث بأنّه قائم الزوايا عندما يكون قياس إحدى زواياه يساوي 90 درجة، وعليه فالمعادلة تُصبح:
- س+ص+90=180.
- ومنه س+ص=90، حيث س، ص هما زوايا المثلث القائم غير القائمتين.
- حساب زوايا المثلث متساوي الساقين: يُسمّى المثلث متساوي الساقين بهذا الاسم نظرًا لأنّ قياس زوايا القاعدة فيه متساوية، وعليه فإنّ مجموع زوايا هذا المثلث هي على النحو الآتي:
- 2×س+ص= 180، حيث أنّ س هو قياس زاويتي القاعدة، وص قياس زاوية الرأس.
- حساب زوايا المثلث متساوي الأضلاع: يُمكن تعريف المثلث متساوي الأضلاع على أنّه مثلث متساوي الأضلاع ومتساوي الزوايا أيضًا؛ إذ إنّ قياس كل زاوية من زواياه يساوي دائمًا 60 درجة، وعليه فإنّ:
- س+س+س= 180.
- ومنه 3×س= 180.
- بقسمة الطرفين على الرقم 3، ينتج أنّ قيمة س= 60 درجة.
أنواع زوايا المثلث
تتعدد أنواع زوايا المثلث وتتنوع، ويُمكن تصنيف المثلث حسب قياس الزوايا الداخليّة الخاصّة به، كما يلي:[٢]
مُثلث قائم الزاوية
يُطلق اسم المُثلث قائم الزاوية (بالإنجليزية: Right Triangle) على المُثلث الذي يكون لديه زاوية قائمة واحدة ويكون قياسها 90 درجة.
مُثلث منفرج الزاوية
يُوصف المثلث بأنّه مُثلث منفرج الزاوية (بالإنجليزية: Obtuse Triangle) عندما يمتلك زاوية مُنفرجة واحدة، أي أكبر من 90 درجة.
مُثلث حاد الزوايا
يُعرف المُثلث الذي لديه 3 زوايا حادة بأنّه مُثلث حاد الزوايا (بالإنجليزية: Acute Triangle)، ويُكون قياس الزاوية الحادة أقل من 90 درجة.
يجب تحديد نوع المثلث قبل البدء بحساب قياس زواياه، فحساب قياس زوايا المثلث الحاد يختلف عن المثلث منفرج الزاوية أو المثلث قائم الزاوية.
أمثلة لإيجاد قياس الزوايا المجهولة في المثلث
فيما يلي بعض الأسئلة والحلول حول حساب زوايا المُثلث:[٣]
المثال الأول
- السؤال: ما هو قياس الزاوية أ، الواقعة في المُثلث أ ب ج، إذا كان قياس الزاوية ب يُساوي 32 درجة، وقياس الزاوية ج يُساوي 24 درجة.[٤]
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه فإنّ:
- أ + (24 +32)= 180.
- س+56 =180.
- س =180-56.
- ومنه: س =124 درجة.
المثال الثاني
- السؤال: مُثلث يحتوي على زاوية قياسها 70 درجة، وزاوية أُخرى قياسها 50 درجة، فما هو قياس الزاوية الثالثة؟[٣]
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه فإنّ:
- س+ (70+50)= 180.
- س =180-120.
- ومنه: س =60 درجة.
المثال الثالث
- السؤال: مُثلث يحتوي على زاوية قياسها 80 درجة، وزاوية أُخرى قياسها 50 درجة، فما هو قياس الزاوية الثالثة؟[٣]
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه:
- س +80 +50= 180.
- س =180-130.
- ومنه: س =50 درجة.
المثال الرابع
- السؤال: المثلث هـ و ي، هو مُثلث له زاوية مُنفرجة قياسها 120 درجة واسمها (هـ)، ويحتوي على زاوية أُخرى اسمها (و) قياسها 35 درجة، ما هو قياس الزاوية (ي)؟[٣]
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه فإنّ:
- ي+120+35 =180
- ي =180-155
- ومنه، ي =25 درجة.
المثال الخامس
- السؤال: المُثلث أ ب ج يحتوي على الزاوية أ وقياسها 17 درجة، والزاوية ب قياسها 38 درجة، فما هو قياس الزاوية ج الموجودة في هذا المثلث؟
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه فإنّ:
- ج +17 +38 =180
- ج =180-55
- ومنه، ج = 125 درجة.
المثال السادس
- السؤال: مُثلث ف ق ك يحتوي على زاوية اسمها ف وقياسها 91 درجة، وزاوية أُخرى اسمها ق وقياسها 41 درجة، فما هو قياس الزاوية ك الموجودة في هذا المثلث؟[٣]
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه:
- ك +91 +41 =180،
- ك =180 -132،
- ومنه: ك =48 درجة.
المثال السابع
- السؤال: المُثلث أ ب ج يحتوي على الزاوية أ وقياسها 7س-5 درجة، والزاوية ب قياسها 2س+3 درجة، والزاوية ج قياسها 6س-13، فما هو قياس زوايا هذا المثلث؟
- الحل: مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة، وعليه: (7س-5) + (2س+3) + (6×س-13) =180، وبترتيب المعادلة وجمع الحدود المتشابهة ينتج أن: 15س-15=180، 15س=195، ومنه: س= 13، وبتعويض قيمة س في قيم الزوايا ينتج أن:
-
- قياس الزاوية أ= 7س-5 = 7(13)-5= 86 درجة.
- قياس الزاوية ب= 2س+3 = 2(13)+3= 29 درجة.
- قياس الزاوية ب= 6س-13 = 6(13)-13= 65 درجة.
المثال الثامن
- السؤال: مُثلث مُتساوي الساقين، قِيمة الزاوية ج فيه تساوي 80 درجة، وقِيمة الزاويتين أ و ب المجاورتين للساقين المتساويتين غير معلومتين، فما هو قياسهما؟[٣]
- الحل: بِما أنّ المُثلث مُتساوي الساقين، فإنَّ الزاويتين المجاورتين للساقين المُتساويتين متساويتان أيضًا، وعليه فأنّ:
- مجموع زوايا المثلث متساوي الساقين= 2×س+ص= 180
- وبتعويض قيمة الزاوية المعلومة (80)، ينتج أنّ: 2×س+80= 180
- وبحل المعادلة ينتج أنّ قيمة س تُساوي 50 درجة، أي أنّ الزاوية أ تُساوي 50 درجة، والزاوية ب تُساوي 50 درجة.
المثال التاسع
- السؤال: إذا كانت الزاوية هـ زاوية خارجة عن المثلث أب ج، وتقع بين امتداد القاعدة (ب ج)، والضلع (أب)، جد قياس الزاوية هـ علمًا أنّ قياس الزاوية أ= 61 درجة، وقياس الزاوية ج= 65 درجة.[٣]
- الحل: قياس الزاوية الخارجة عن المثلث يساوي مجموع الزاويتين الداخليتين البعيدتين
- وعليه فإنّ قياس الزاوية هـ= قياس أ+ قياس ج = 65+61= 126 درجة.
المثال العاشر
- السؤال: إذا كانت الزاوية هـ زاوية خارجة عن المثلث أب ج، وتقع بين امتداد القاعدة (ب ج)، والضلع (أب)، وكان قياس الزاوية هـ 124، وقياس الزاوية ج 77 درجة، فما هو قياس الزاوية أ.[٥]
- الحل: قياس الزاوية الخارجة عن المثلث يساوي مجموع الزاويتين الداخليتين البعيدتين
- وعليه فإنّ قياس الزاوية هـ= قياس أ+ قياس ج
- ومنه: 124=77+ قياس الزاوية ج
- ومنه قياس الزاوية ج= 124-77= 47 درجة.
المثال الحادي عشر
- السؤال: المُثلث أ ب ج يحتوي على الزاوية أ وقياسها 57 درجة، والزاوية ج قياسها 85 درجة، رُسم فيه خط مستقيم موازٍ للقاعدة (ب ج)، ويقطع الضلعين أب، أج في النقطتين د، هـ على الترتيب، فما هو قياس الزاوية أدهـ.[٥]
- الحل: الزاوية أدهـ تساوي في قياسها الزاوية ب؛ لأنهما زاويتان متناظرتان
- وعليه يجب حساب قياس الزاوية ب، حيث إنّ مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة
- وعليه: ب+57 +85 =180، ب =180-142
- ومنه: ب =38 درجة= الزاوية أدهـ.
المثال الثاني عشر
- السؤال: المُثلث أ ب ج قائم الزاوية في ب، والزاوية أج ب قياسها 40 درجة، رُسم خط مستقيم من الزاوية القائمة ب نحو منتصف الضلع أ ج قاطعاً إياه بالنقطة د، إذا كان ب د= أد = دج، جد قياس الزاوية أدب.[٦]
- الحل: وفق خصائص المثلث متساوي الساقين فإنّ زوايا القاعدة متساويتان
- وعليه المثلث دب ج مثلث متساوي الساقين فيه الزاوية أج ب= الزاوية دب ج = 40 درجة، بينما الزاوية د ب ج زاوية خارجة عن المثلث د ب ج، وتساوي مجموع الزاويتين الداخليتين البعيدتين
- أي أدب=دب ج +أج ب= 40+40=80 درجة، وهو قياس الزاوية أدب.
تختلف طريقة حساب قياسات زوايا المثلث، بحبس نوع المثلث، إذ يوجد المثلث متساوي الأضلاع والمثلث متساوي الساقين والمثلث قائم الزاوية، كما ويمكن تصنيف المثلثات حسب نوع الزوايا إلى مثلث حاد الزاوية ومنفرج الزاوية وقائم الزاوية، وعند حساب زوايا المثلث، يجب اللجوء للقانون المناسب حسب نوع المثلث.
المراجع
- ^ أ ب "Triangles Contain 180°", mathsisfun, Retrieved 1-8-2021. Edited.
- ↑ "Types Of Triangles", byjus, Retrieved 13/7/2021. Edited.
- ^ أ ب ت ث ج ح خ "Finding Angles in Triangles", cimt, Retrieved 1-8-2020. Edited.
- ↑ "Interior Angles Of A Triangle", Online Math Learning, Retrieved 1/7/2021. Edited.
- ^ أ ب "The angle sum of a Triangle is 180° - lesson with proof & varied exercises", Home School Math, Retrieved 1/7/2021. Edited.
- ↑ "Triangles Contain 180 Degrees ", Math Opolis, Retrieved 1/7/2021. Edited.