محتويات

نص قانون المثلث القائم
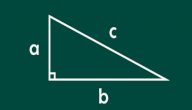
يُعرف المثلث قائم الزاوية (بالإنجليزية: Right Angled Triangle) بأنه مثلث ذو زاوية بقياس 90ْ درجة، وتكون هذه الزاوية محصورة بين الضلع القائم وقاعدة المثلث، بينما يمثل ضلعه الثالث الوتر.[١]
ومن المعروف أن مجموع زوايا المثلث يساوي 180ْ درجة، أي أن مجموع الزاويتين المتبقيتين يساوي 90ْ درجة، ويمتاز عن غيره من المثلثات بارتباط أضلاعه بصيغة رياضية تُدعى نظرية فيثاغورس وهي قانون المثلث قائم الزاوية.[١]
والصيغة الرياضية الآتية توضح قانون المثلث قائم الزاوية على اعتبار أن المثلث س ص ع قائم الزاوية في ص:[١]
بالكلمات:
(الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
وبالرموز:
(س ع)2 = (س ص)2 + (ص ع)2
الصيغة العامة لحساب مساحة المثلث قائم الزاوية
تمثل مساحة المثلث المساحة المحصورة بداخله أو بين أضلاعه، والتي تحسب بالوحدات المربعة، وفيما يأتي الصيغة العامة لحساب مساحة مثلث قائم الزاوية على اعتبار وجود مثلث قائم الزاوية ذو قاعدة (س)، والضلع المعامد لها (ص)، والوتر الواصل بينهما (ع):[٢]
بالكلمات:
مساحة المثلث = (1/2) × طول القاعدة × الارتفاع
وبالرموز:
م (س ص ع) = (1/2) × س × ص
إذ إن:[٢]
- س: ضلع القاعدة (سم، متر....).
- ص: الضلع المتعامد على القاعدة، ويمثل الارتفاع (سم، متر....).
- م: مساحة المثلث ووحدتها (سم2، متر2......).
خطوات إثبات أنّ المثلث قائم الزاوية
يمكن معرفة ما إذا كان المثلث قائم الزاوية أم لا بتطبيق قانون مثلث قائم الزاوية الذي يربط أضلاع المثلث بنظرية فيثاغورس، ويمكن استخدام قانون حساب مساحته لإيجاد أطوال الأضلاع المجهولة فيه لاستخدامها في نظرية فيثاغورس.[٢]
فيما يأتي أمثلة لإثبات ما إذا كان المثلث يشكل مثلث قائم الزاوية أم لا:
المثال الأول: حدد ما إذا كان المثلث ذو الأضلاع 6 سم، 8 سم، 10 سم، هو مثلث قائم الزاوية أم لا؟[٣]
الحل:
- لكي يكون المثلث قائم الزاوية؛ يجب تطبيق معادلة فيثاغورس والتأكد من أن الأضلاع تحقق هذه المعادلة كما يأتي:
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- يُعامل أطول ضلع على أنه الوتر، لأن من المفروض أن يكون أطول ضلع في مثلث قائم الزاوية هو الوتر.
- (10)2 = (6)2 + (8)2
- 100 = 36 + 64
- 100 = 100
- لقد تحققت المعادلة؛ إذًا المثلث يعتبر قائم الزاوية.
المثال الثاني: حدد ما إذا كان المثلث ذو الأضلاع 5 سم، 7 سم، 9 سم، مثلث قائم الزاوية أم لا؟[٣]
الحل:
- أيضًا يجب أن تحقق المعطيات الآتية قاعدة فيثاغورس، ليكون المثلث قائم الزاوية:
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (9)2 = (5)2 + (7)2
- 81 = 25 + 49
- 81 > 74
- المثلث لا يعتبر قائم الزاوية لعدم تحقيق المعادلة.
أمثلة حسابية على قانون المثلث قائم الزاوية
فيما يأتي أمثلة حسابية متعددة على قانون المثلث قائم الزاوية.
عندما يكون الوتر معلومًا
المثال الأول: إذا كان الوتر في مثلث قائم الزاوية يساوي 13 سم، والقاعدة فيه تساوي 12 سم، أوجد الضلع العامودي القائم على القاعدة في المثلث.[٤]
الحل:
- بتطبيق القانون الذي يربط أطوال أضلاع المثلث قائم الزاوية:
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (13)2 = (12)2 + (الضلع العامودي المجهول)2
- 169 = 144 + (الضلع العامودي المجهول)2
- 169 - 144 = (الضلع العامودي المجهول)2 ؛ بأخذ الجذر التربيعي للطرفين تصبح المعادلة كما يلي:
- 25√ = الضلع العامودي
- 5 سم = الضلع العامودي في المثلث القائم الزاوية
المثال الثاني: مثلث س ص ع مثلث قائم الزاوية في ص، طول الضلع س ص = 3 سم، والضلع ص ع = 4 سم، والوتر س ع = 5 سم، فما مساحة المثلث؟[٥]
الحل:
- بتطبيق الصيغة العامة.
- م (س ص ع) = (1/2) × س ص × ص ع
- م = (1/2) × (3) × (4)
- م = (1/2 ) × 12
- م = 6 سم2
- لا علاقة للوتر في قانون مساحة المثلث قائم الزاوية؛ لكن هناك علاقة بين هذا القانون وأطوال الأضلاع الأخرى في المثلث.
عندما يكون الوتر مجهولًا
المثال الأول: إذا كان أحد أضلاع مثلث قائم الزاوية يساوي 8 سم، والضلع العامودي عليه يساوي 6 سم، فكم يبلغ طول وتر المثلث؟[٤]
الحل:
- بتطبيق القانون الذي يربط أطوال أضلاع المثلث قائم الزاوية:
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (الوتر)2 = (8)2 + (6)2
- (الوتر)2 = 64 + 36
- الوتر = (100)2
- الوتر = 10 سم
يمكن حل المثلث قائم الزاوية، وإيجاد أحد أضلاعه المجهولة بتطبيق قانونه، كما يمكن إثبات أنه قائم أم لا، عند تحقيق أضلاعه للصيغة العامة للمثلث، بحيث يكون الوتر أطول ضلع فيه، وكذلك يمكن إيجاد محيط المثلث القائم الزاوية بسهولة أيضًا.
المراجع
- ^ أ ب ت "Right Angled Triangle", BYJU'S, Retrieved 19/6/2021. Edited.
- ^ أ ب ت "Area of Right Triangle", Cuemath, Retrieved 19/6/2021. Edited.
- ^ أ ب "The Converse of Pythagorean Theorem", Varsity Tutors, Retrieved 24/6/2021. Edited.
- ^ أ ب "Right Angled Triangle", BYJU'S, Retrieved 24/6/2021. Edited.
- ↑ "Basic Geometry : How to find the area of a right triangle", Varsity Tutors, Retrieved 19/6/2021. Edited.