محتويات

حساب محيط المثلث القائم
وفيما يأتي كيفية حساب محيط المثلث قائم الزاوية (بالإنجليزية: Right Triangle):
باستخدام القانون العام
يمكن حساب محيط المثلث الذي أطوال أضلاعه أ، وب، وجـ من خلال حساب مجموع هذه الأطوال، وذلك كما يلي:[١]
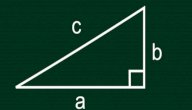
- محيط المثلث = أ + ب + جـ، حيث:
- أ، ب: هما طول ضلعي القائمة.
- جـ: هو طول الوتر في المثلث القائم.
بالاستعانة بنظرية فيتاغورس
ويمكن التعبير عن هذا القانون بطريقة أخرى، وذلك كما يلي:[١]
- تنص نظرية فيثاغورس على أن مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر، أي أن: جـ²= أ²+ب²، وبالتالي فإن جـ = (أ²+ب²)√.
- بتعويض قيمة الوتر في قانون المحيط: محيط المثلث القائم = أ+ب+جـ فإن محيط المثلث هو:
- محيط المثلث القائم = أ+ب+(أ²+ب²)√، وذلك لحساب محيط المثلث دون معرفة الوتر؛ حيث إن:
- أ، ب: طول ضلعي القائمة.
- محيط المثلث القائم = أ+ب+(أ²+ب²)√، وذلك لحساب محيط المثلث دون معرفة الوتر؛ حيث إن:
أمثلة على حساب محيط المثلث قائم الزاوية
وفيما يأتي أمثلة متنوعة على حساب محيط المثلث قائم الزاوية:
- المثال الأول: مثلث قائم الزاوية أضلاعه هي: 3، 4، 5سم، جد محيطه.[٢]
الحل:
- بتطبيق القانون: محيط المثلث = مجموع أطوال أضلاعه= أ+ب+جـ = 3+4+5 = 12سم.
- المثال الثاني: مثلث قائم الزاوية أضلاعه هي: 6، 8، 10م، جد محيطه.[٢]
الحل:
- بتطبيق القانون: محيط المثلث = مجموع أطوال أضلاعه= أ+ب+جـ = 6+8+10 = 24م.
- المثال الثالث: مثلث قائم الزاوية طول أحد ضلعيه (ب) يساوي 4/3 من طول الضلع الآخر (أ)، وطول الوتر(جـ) يساوي 30 م، فما هو طول ضلعي القائمة، وما محيط المثلث القائم؟[١]
الحل:
- نفرض أن طول الضلع (أ) = س، وبالتالي فإن طول الضلع ب = 4/3×س.
- تطبيق نظرية فيثاغورس لإيجاد طول ضلعي القائمة كما يلي:
- جـ² = أ² + ب²، 30² =س²+(4/3×س)²، س²+(16/9)س²=900، 25/9 س²=900، وبحل المعادلة ينتج أن: س= 18م، وبالتالي فإن طول الضلع (أ) = 18م.
- طول الضلع (ب) = 4/3×س = 4/3×18= 24م.
- محيط المثلث = مجموع أطوال أضلاعه، ويمكن إيجاد المحيط كما يلي:
- محيط المثلث = أ + ب + جـ = 18+24+30 = 72 م.
- المثال الرابع: ما هو محيط المثلث القائم الذي طول الوتر فيه (جـ) يساوي 8سم، وطول أحد ضلعيه (أ) يساوي 5سم؟[٢]
الحل: محيط المثلث القائم = مجموع أطوال أضلاعه.
- لحساب المحيط فإنه يجب إيجاد طول الضلع الثالث (ب) للمثلث، وذلك باستخدام نظرية فيثاغورس كما يلي:
- جـ² = أ² + ب²، 8² = 5² + ب²، 64 = 25 + ب²، ومنه: ب= 39√= 6.24 سم.
- بعد إيجاد طول الضلع الثالث يمكن حساب محيط المثلث القائم كما يلي:
- محيط المثلث = أ + ب + جـ = 5+6.24+8= 19.24سم.
- المثال الخامس: إذا كان طول أحد ضلعي المثلث القائم يزيد عن طول الضلع الآخر بمقدار 200سم، وطول الوتر (جـ) فيه يساوي 1000سم، فما هو طول ضلعي القائمة، وما هو محيط المثلث القائم؟[١]
الحل:
- لنفرض أن طول الضلع الأول (أ)= س، وبما أن طول الضلع الثاني (ب) يزيد عن طول الضلع الأول بمقدار 200، فإن ب= 200+س.
- يمكن تطبيق نظرية فيثاغورس لإيجاد طول ضلعي القائمة كما يلي:
- جـ² = أ² + ب²، (1000)² = س² + (س+200)²، وبفك الأقواس وترتيب المعادلة ينتج أن: 2س²+400س- 960,000=0، وبحل هذه المعادلة التربيعية ينتج أن: س= 600، وس= -800، وبما أن س تمثل طول الضلع أ، ولا يمكن للطول أن يكون سالباً، فإنه يجب إهمال قيمة س= -800.
- طول الضلع أ يساوي 600سم، وطول الضلع ب= س+200= 200+600 = 800 سم.
- محيط المثلث القائم يساوي مجموع أطوال أضلاعه، ويمكن إيجاده كما يلي:
- محيط المثلث = أ + ب + جـ = 600 + 800 + 1000= 2,400 سم.
- المثال السادس: ما هو محيط المثلث قائم الزاوية الذي طول الوتر فيه 50سم، علماً أن المثلث متساوي الساقين؟[١]
الحل: محيط المثلث يساوي مجموع أطوال أضلاعه، ولحساب طول هذه الأضلاع يجب اتباع ما يلي:
- يمكن إيجاد طول الضلعين المتساويين اللذين يمثلان ضلعي القائمة باستخدام نظرية فيثاغورس، وذلك كما يلي:
- الوتر²= (الضلع الأول)²+(الضلع الثاني)²، ومنه: 50² = 2×(طول أحد الضلعين)²، وذلك لأن الضلعين متساويان في الطول، ومنه: 2500 = 2×طول أحد الضلعين²، وبالقسمة على (2)، وأخذ الجذر التربيعي للطرفين ينتج أن طول الضلعين المتساويين= 1250√ سم.
- أصبحت جميع أطوال أضلاع المثلث القائم معروفة، وبالتالي يمكن إيجاد المحيط كما يلي:
- محيط المثلث = الوتر + طول ضلعي القائمة = 50 + (2×1250√)= 120.7سم تقريباً.
- المثال السابع: مثلث قائم أ ب جـ فيه طول الوتر أج = 6سم، وطول الضلع أب= (5س)√، وطول الضلع ب جـ= س، فما هو محيطه؟[٣]
الحل:
- يمكن استخدام نظرية فيثاغورس لإيجاد قيمة س، وذلك كما يلي:
- أج² = ب جـ² + أ ب²، 6² = (5س√)² + س²، 36 = 5س+س²، س² + 5س-36=0، وبتحليل المعادلة التربيعية إلى عواملها فإن: (س+9)(س-4)=0، وبالتالي فإن س لها قيمتان، وهما: س= -9، وس= 4، والقيمة الأولى تُهمل، وذلك لأن الطول لا يمكن أن يكون سالباً.
- طول الضلع ب جـ =4سم، أب= (5س)√ = (5×4)√ = (5)√2 سم.
- محيط المثلث القائم يساوي مجموع أطوال أضلاعه، ويمكن إيجاده كما يلي:
- محيط المثلث = أب + ب جـ + أ جـ = (5)√2+4+6= 10+5√2 سم.
- المثال الثامن: مثلث متساوي الساقين وقائم الزاوية فيه طول الوتر 2√8 سم، ما هو محيطه؟[٤]
الحل: بما أن المثلث متساوي الساقين، وقائم الزاوية، فإنه يمكن إيجاد طول الضلعين المتساويين اللذين يمثلان ضلعي القائمة كما يلي:
- الوتر²= (الضلع الأول)²+(الضلع الثاني)²، ومنه: (2√8)²= 2×(طول أحد الضلعين)²، وذلك لأن الضلعين متساويان في الطول، ومنه: 192= 2×طول أحد الضلعين²، وبقسمة الطرفين على (2)، وأخذ الجذر التربيعي للطرفين ينتج أن: طول الضلعين المتساويين= 8 سم.
- محيط المثلث القائم = 2×طول أحد ضلعي القائمة + طول الوتر = 2×8 + 2√8= 16+2√8 سم.
المراجع
- ^ أ ب ت ث ج "Area and Perimeter of Right Triangles Problems With Solution", www.analyzemath.com, Retrieved 20-4-2020. Edited.
- ^ أ ب ت "Perimeter of Right Triangle", www.math-salamanders.com, Retrieved 20-4-2020. Edited.
- ↑ "How to find the perimeter of a right triangle", www.varsitytutors.com, Retrieved 20-4-2020. Edited.
- ↑ "perimeter of the isosceles right angled triangle", www.toppr.com, Retrieved 20-4-2020. Edited.