محتويات

كيفية حساب مساحة الأشكال ثنائية الأبعاد
تُعرّف المساحة على أنها المنطقة المحصورة داخل حدود الشكل الهندسي، ومن الممكن إيجاد مساحة أي شكل بعدة طرق تتمثل أبسطها وأكثرها بدائيّة بطريقة العد؛ وتكون عن طريق رسم الشكل ثنائي الأبعاد على ورق بياني (مربعات)، ومن ثم عد المربعات التي يشغلها هذا الشكل، حيث يُمثل كل مربع منها وحدة مربّعة، ويتم تحديد الوحدة المُراد استخدامها في قياس مساحة الشكل.[١][٢]
مثال توضيحي:
لو كان الشكل المرسوم على هذه الورقة مستطيلاً، وكانت الوحدة المُستخدمة لرسم المربعات (1 سم)، وطُلب إيجاد مساحته، فيتم عندها ببساطة عدّ المربّعات الموجودة داخل المستطيل (على فرض أنها 8 مربعات)، ثَم كتابة الناتج مرافقاً للوحدة المربعة على الشكل الآتي:
مساحة المستطيل=8 سم²، كما يُمكن إيجاد المساحة أيضاً من خلال صيغ وقوانين محددة لكل شكل يتم من خلالها حساب المساحة بطريقة بسيطة، ومن أبرز الأمثلة عليها ما يأتي:[١][٢]
مساحة المربع
يُعرّف المربع على أنّه شكل هندسي ثنائي الأبعاد، وجميع أضلاعه متساوية في الطول، وكذلك فإنّ زواياه الأربعة قائمة ومتساوية،[٣] أما بالنسبة لمساحته فهي عبارة عن طول الضلع مرفوعاً للقوة 2؛ أي طول الضلع مضروباً بنفسه؛ وبذلك فإنّ:[٤][٥]
مساحة المربع = (طول الضلع)²
ومن الأمثلة التي توضح كيفية حساب مساحة المربّع ما يأتي:
مثال: احسب مساحة مربع، إذا علمت أن طول ضلعه يساوي 8م.[٥]
الحل:
- باستخدام قانون مساحة المربع، فإن: مساحة المربع= (8)²= 64م².
مساحة المستطيل
يُعرف المستطيل بأنّ أطوال أضلاعه غير متساوية ككل، وفيه الزوجان المتقابلان من أضلاعه فقط متساويان، أما زواياه الأربعة فهي قائمة ومتساوية،[٦] أما بالنسبة لمساحته فهي عبارة عن حاصل ضرب الطول في العرض؛ أي:
مساحة المستطيل= الطول × العرض
ومن الأمثلة التي توضّح كيفية حساب مساحة المستطيل ما يأتي:[٧]
مثال: احسب مساحة بطاقة مستطيلة الشكل، إذا علمت أنّ طولها يساوي 5 سم، أما عرضها فيساوي 3 سم.
الحل:
- مساحة المستطيل= الطول× العرض= 3×5= 15 سم².
مساحة الدائرة
يُمكن حساب مساحة الدائرة عن طريق استخدام القانون الآتي:
مساحة الدائرة = π×نصف القطر²
ومن الأمثلة التي توضّح كيفية حساب مساحتها ما يلي:[٨]
مثال: احسب مساحة الدائرة، إذا علمت أن طول نصف قطرها يساوي 4 سم.
الحل:
- مساحة الدائرة = π×نصف القطر²= 3.14×4²= 50.24 سم².
مساحة المثلث
يُمكن حساب مساحة المثلث مهما اختلفت أنواعه عن طريق استخدام القانون الآتي:
مساحة المثلث= 1/2×طول القاعدة×الارتفاع
ومن الأمثلة التي توضّح كيفية حساب مساحته ما يأتي:[٨]
مثال: احسب مساحة المثلث، إذا علمت أن طول قاعدته يساوي 6 سم، وارتفاعه وهو العمود الساقط من الرأس المقابل للقاعدة نحوها 6سم.
الحل:
- مساحة المثلث= 1/2×طول القاعدة×الارتفاع= 1/2×6×4= 12 سم².
مساحة المعين
يُمكن حساب مساحة المعين عن طريق استخدام القانون الآتي:
مساحة المعين= 1/2×طول القطر الأول×طول القطر الثاني
ومن الأمثلة التي توضّح كيفية حساب مساحته ما يأتي:[٨]
مثال: احسب مساحة المعين، إذا علمت أن طول قطره الأول يساوي 3سم، وطول قطره الثاني يساوي 5سم.
الحل:
- مساحة المثلث= 1/2×طول القطر الأول×طول القطر الثاني= 1/2×3×5= 7.5 سم².
مساحة متوازي الأضلاع
يمكن حساب مساحة متوازي الأضلاع عن طريق استخدام القانون الآتي:
مساحة متوازي الأضلاع= طول القاعدة×الارتفاع
حيث يُمثّل الارتفاع المسافة العمودية بين القاعدة والضلع المقابل لها، ومن الأمثلة التي توضّح كيفية حساب مساحته ما يأتي:[٨]
مثال: احسب مساحة متوازي الأضلاع، إذا علمت أن طول قاعدته يساوي 6سم، وارتفاعه يساوي 4سم.
الحل:
- مساحة متوازي الأضلاع= طول القاعدة×الارتفاع = 6×4=24 سم².
مساحة شبه المنحرف
يمكن حساب مساحة شبه المنحرف عن طريق استخدام القانون الآتي:
مساحة شبه المنحرف=1/2×مجموع طول القاعدتين×الارتفاع
حيث إن القاعدتان هما الضلعان المتوازيان في شبه المنحرف، أما الارتفاع فهو المسافة العمودية الواصلة بينهما، ومن الأمثلة التي توضّح كيفية حساب مساحته ما ]أتي:[٨]
مثال: احسب مساحة شبه المنحرف، إذا علمت أن طول قاعدتيه يساوي 6سم، 3سم، وارتفاعه يساوي 4سم.
الحل:
- مساحة شبه المنحرف= 1/2×مجموع طول القاعدتين×الارتفاع= 1/2×(6+3)×4=18 سم².
كيفية حساب مساحة المجسّمات ثلاثية الأبعاد
تُعرف المجسمات على أنّها أشكال صلبة ذات أبعاد ثلاثية: طول، وعرض، وارتفاع، وهناك عدة أنواع من المجسمات؛ كالأسطوانة، والمنشور، أما طُرق إيجاد المساحة السطحية للمجسمات فهي تتم من خلال معرفة طبيعة الأشكال الهندسية المكوِّنة للمجسم، ومن ثَم حساب مساحة كل وجه على حدة، ثم جمع المساحات كاملة، أو من خلال اعتماد صيغ وقوانين محددة تُستخدم لإيجاد المساحات في بعض الأشكال المعروفة كما يأتي:
مساحة سطح الأُسطوانة
الأسطوانة هي مجسم ثلاثي الأبعاد فيه قاعدتان دائريتان متقابلتان ومتطابقتان، كما أنّ جوانبه عبارة عن مستطيل ملتف بين القاعدتين،[٩] وتُحسب مساحة الإسطوانة بالقانون الآتي:
مساحة الأسطوانة= محيط القاعدة×الارتفاع+ 2×مساحة القاعدة
وبما أنّ القاعدة الواحدة عبارة عن دائرة، فإنّ:
مساحة سطح الأسطوانة= 2×π×نصف قطر القاعدة ×الارتفاع+2×π×نصف قطر القاعدة²
علماً بأنّ:
محيط الدائرة= 2×π×نق
أمّا:
مساحة الدائرة = π×نق²
ومن الأمثلة التي توضح كيفية حساب مساحة الأسطوانة ما يأتي:[١٠]
مثال: احسب مساحة الأسطوانة إذا علمت أن نصف قطر قاعدتها يساوي 5م، أما ارتفاعها فيساوي 7م.
الحل:
- مساحة الأسطوانة = (2×π×نق)×الارتفاع+2×(π×نق²) = 2×3.14×5×7 + 2×3.14×5² = 376 م².
مساحة سطح متوازي المستطيلات
متوازي المستطيلات هو منشور قائم، تحتوي أوجهه الجانبية على مستطيلات، فيه كل زوج من الأوجه المتقابلة متطابقة، بما فيها القاعدتان، أما مساحة سطحه فتساوي:
مساحة سطح متوازي المستطيلات= محيط القاعدة×الارتفاع+ 2×مساحة القاعدة
وبما أنّ القاعدة الواحدة عبارة عن مستطيل، فإن:
المساحة الكلية لمتوازي المستطيلات = 2×(الطول+العرض)×الارتفاع+2×(الطول×العرض)
ومنه:
المساحة الكلية لمتوازي المستطيلات = 2×(الطول×العرض)+ 2×(العرض×الارتفاع)+ 2(الطول×الارتفاع)
علماً بأنّ:
محيط المستطيل= 2×الطول+ العرض
أمّا
مساحة المستطيل= الطول×العرض
ومن الأمثلة التي توضح كيفية حساب مساحة متوازي المستطيلات ما يأتي:[١١][٤]
مثال: احسب مساحة سطح متوازي المستطيلات، إذا علمت أن طول قاعدته 3سم، وعرضها 4سم، أما ارتفاعه فيساوي 10سم.
الحل:
- مساحة سطح متوازي المستطيلات= 2×(الطول+العرض)×الارتفاع+ 2×(الطول×العرض)= 2(3+4)×10+ 2×(4×3) = 164سم².
مساحة سطح الهرم
يُعتبر الهرم من المجسمات الثلاثية الأبعاد حيث يحتوي على قاعدة واحدة فقط على شكل مضلع منتظم، وأوجهه الجانبية عبارة عن مثلثات عددها مقرون بعدد أضلاع القاعدة، أما حساب مساحة سطحه فهي عبارة عن مجموع مساحات أوجهه المثلثة بالإضافة إلى مساحة القاعدة، كالآتي:[٩]
المساحة الجانبية للهرم= مساحة المثلث الواحد (الأوجه الجانبية)×عدد المثلثات
أمّا:
مساحة سطح الهرم الكلية= مساحة المثلث الواحد (الأوجه الجانبية)×عدد المثلثات + مساحة القاعدة.
من الأمثلة التي توضح كيفية حساب مساحة الهرم ما يأتي:
مثال: احسب المساحة الكلية لهرم رباعي، إذاعلمت أن ارتفاعه الجانبي يساوي 17م، أما طول ضلع قاعدته فيساوي 16م.[١٢]
الحل:
- قاعدة هذا الهرم مربعة الشكل، أما عدد أوجهه المثلثة الجانبية فهو (4)، وعليه: مساحة سطح الهرم الكلية= مساحة المثلث الواحد (الأوجه الجانبية) ×عدد المثلثات + مساحة القاعدة = (1/2×16×17)×4 + 16×16 = 800م².
مساحة سطح الكرة
تُمثل الكرة مجموعة من النقاط الواقعة على بعد ثابت هو نصف قطرها من نقطة معينة تُعرف باسم مركز الكرة، ويُمكن حساب مساحة سطح الكرة ببساطة عن طريق اتباع القانون الآتي:[٩]
مساحة الكرة = 4×π×نصف القطر²
ومن الأمثلة التي توضح كيفية حساب مساحتها ما يأتي:[١٣]
مثال: احسب المساحة الكلية لكرة، إذاعلمت أن نصف قطرها يساوي 4سم.
الحل:
- مساحة الكرة = 4×π×نصف القطر² = 4×3.14×4² = 200.96 سم².
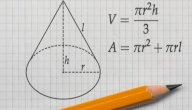
مساحة سطح المخروط
المخروط هو عبارة عن هرم قاعدته دائرية الشكل، وسطحه منحنٍ، ويُمكن حساب مساحته ببساطة عن طريق اتباع القانون الآتي:[٩]
مساحة المخروط= π×نصف قطر القاعدة×(نصف قطر القاعدة+الارتفاع الجانبي)
ومن الأمثلة التي توضح كيفية حساب مساحته ما يأتي:[١٤]
مثال: احسب المساحة الكلية لمخروط، إذاعلمت أن نصف قطر قاعدته يساوي 4سم، وارتفاعه الجانبي 5سم.
الحل:
- مساحة المخروط= π×نصف قطر القاعدة×(نصف قطر القاعدة+الارتفاع الجانبي) = 3.14×4×(4+5) = 113 سم².
مساحة سطح المنشور
المنشور المنتظم القائم هو مجسم ثلاثي الأبعاد تُمثّل كل من قاعدتيه المتطابقتين والمتوازيتين مضلعاً منتظم الشكل؛ فقد تكون مثلثاً، أو مربعاً، او مستطيلاً، أو غيره، أما أوجهه الجانبية فهي عبارة عن مستطيلات، أما عن حساب مساحته فيتم عن طريق جمع مساحة القاعدتين مع مساحة الأوجه الجانبية، وذلك من خلال القانون الآتي:
مساحة المنشور= 2×مساحة القاعدة + محيط القاعدة×ارتفاع المنشور
ومن الأمثلة التي توضح كيفية حساب مساحته ما يأتي:[١٥]
مثال: احسب المساحة الكلية لمنشور، إذاعلمت أن قاعدته على شكل شبه منحرف طول قاعدتيه يساوي 6سم، 12سم، وارتفاعه 4سم، أما طول ساقيه المتساويتين فهو 5سم، وارتفاع المنشور 10سم.
الحل:
- مساحة المنشور= 2×مساحة القاعدة + محيط القاعدة×ارتفاع المنشور = 2× 1/2×(6+12)×4 + (5+5+6+12)× 10 = 352سم².
كيفية حساب المساحة غير المنتظمة
تُعرّف الأشكال غير المنتظمة، بأنّها الأشكال التي تكون غير متساوية الزاويا، وغير متساوية الأضلاع، وقد يكون شكلها مقعّر، أو محدّب، ويوجد عدد كبير ولا نهائي من الأشكال غير المنتظمة،[١٦] وتوجد العديد من الطرق لحساب مساحة الأشكال غير المنتظمة، كما يأتي:
تقسيم الشكل إلى أقسام منتظمة
تشمل هذه الطريقة الخطوات الآتية:[١٧]
- تقسيم الشكل إلى عدة أشكال معروفة وسهلة.
- حساب مساحة هذه الأشكال المقسمة.
- جمع نواتج جميع المساحات، وذلك للحصول على مساحة الشكل غير المنتظم.
مثال توضيحي:
عند حساب مساحة شكل خماسي الأضلاع نقوم بما يأتي:[١٧]
- تقسيم الشكل إلى مستطيل ومثلث.
- إيجاد مساحة المستطيل، والتي تساوي (الطول * العرض).
- إيجاد مساحة المثلث والتي تساوي(0.5 * طول القاعدة *الإرتفاع).
- جمع مساحة المستطيل ومساحة المثلث معًا، للحصول على مساحة خماسي الأضلاع.
استخدام شبكة المربعات
تشمل خطوات حساب مساحة الأشكال غير المنتظمة باستخدام شبكة المربعات ما يأتي:[١٨]
- رسم الشكل على شبكة من المربعات.
- تحديد الإحداثيات السينية والصادية لكل نقطة تُشكّل زاوية من زوايا الشكل.
- توصيل رأسي أو نقطتي كل قطعة مستقيمة مع محور السينات.
- طرح إحداثيات المحور السيني لكل نقطتين من اليسار إلى اليمين للقطعة المستقيمة الواحدة مع الإشارة؛ موجبة أو سالبة.
- حساب متوسط الإرتفاع للقطعة المستقيمة بجمع الإحداثيات الصادية للنقطتين وقسمتها على 2.
- حساب مساحة الشكل الناتج، من خلال ضرب ناتج طرح إحداثيات المحور السيني بناتج الوسط الحسابي لإحداثيات المحور الصادي.
- جمع نواتج مساحات جميع القطع المستقيمة المكوّنة للشكل الهندسي.
استخدام برنامج الأوتوكاد
تشمل خطوات حساب مساحة الأشكال غير المنتظمة باستخدام برنامج الأوتوكاد ما يأتي:[١٩]
- اختيار الأمر مساحة (Area) من قائمة الأوامر، ثم الضغط على مفتاح الإدخال(Enter).
- طباعة الحرف (O)، ثمّ الضغط على مفتاح الإدخال(Enter).
- اختيار الأمر (Object) من قائمة الأوامر، ثم الضغط على مفتاح الإدخال(Enter).
- تحديد الشكل المراد حساب مساحته، وسيقوم البرنامج بإظهارمساحة الشكل و المحيط.
حساب مساحة المنحنيات باستخدام التكامل
تختلف طريقة حساب مساحة المناطق المحدودة ضمن قطع مستقيمة؛ كالمثلث، والمستطيل، والمربع، وغيرها من الأشكال عن طريقة حساب المساحة تحت المنحنيات، أو المساحة المحصورة بينها، حيث يعتمد الرياضيّون على حساب التكامل في إيجاد المنطقة المحصورة بين محور السينات ومنحنى اقترانٍ ما مثلاً، وهناك أكثر من حالة لذلك؛ فأحياناً يكون للمنحنى (أو الاقتران والذي هو الصيغة الرياضيّة للمنحنى) بداية ونهاية معلومتان ومحدّدتان، فبالتالي يسهل الحصول على المساحة هُنا، والتي تتمثل فقط بحساب التكامل لذلك الاقتران، إلّا أنّ بعض الحالات قد تحتاج إلى خطوات أكثر تعقيداً مثل تقسيم المنحنى (الاقتران) إلى أكثر من جزء، ثم حساب التكامل لكل قسم، وجمع الناتج في النهاية، وغيرها الكثير من الحالات.[٢٠]
يُمكن حساب مساحة الأشكال الهندسية المنتظمة وغير المنتظمة بطرق مختلفة، فالأشكال ثنائية الأبعاد يتم حساب مساحتها باستخدام قوانين المساحة الهندسية التابعة لكل شكل، كالمربع، والدائرة وشبه المنحرف، وغيرها، أمّا المجسمات ثلاثية الأبعاد فيُمكن حساب مساحتها بتحديد الأشكال الهندسية الثنائية الأبعاد المكوّنة لها و جمع مساحات هذه الأشكال أو باستخدام قوانين مساحة المجسمات المعروفة، كالهرم، والموشور، وغيرها، كما يُمكن حساب مساحة الأشكال الهندسية غير المنتظمة بتقسيم الشكل الى أشكال منتظمة وحساب مساحتها و جمع المساحات لايجاد المساحة الكلية للشكل، أو باستخدام برنامج الأتوكاد، أو شبكة المربعات، كما يُمكن حساب مساحة الأشكال المنحنية باستخدام التكامل.
المراجع
- ^ أ ب "?What is Area", www.mathsisfun.com, Retrieved 18-12-2017. Edited.
- ^ أ ب "Area: Definition & Counting Method", www.study.com, Retrieved 17-12-2017. Edited.
- ↑ "Square (Geometry)", www.mathsisfun.com, Retrieved 6-5-2020. Edited.
- ^ أ ب رجائي سميح العصار، جواد يونس أبو هليل،محمد زهير أبو صبيح (2013)، مدخل إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_ مكتبة العبيكان، صفحة 85-90، جزء الأول. بتصرّف.
- ^ أ ب "How to Find Perimeter from Area", www.study.com, Retrieved 28-11-2017. Edited.
- ↑ معروف سمحان،نجلاء التويجري،ليان توبان (2016)، رياضيات الأولمبياد: الهندسة (الطبعة الأولى)، الرياض: مؤسسة الملك عبد العزيز للموهبة والإبداع،العبيكان، صفحة 155-180، جزء الأول. بتصرّف.
- ↑ "Area of Plane Shapes", www.mathsisfun.com, Retrieved 6-5-2020. Edited.
- ^ أ ب ت ث ج "Area Of 2 D Shapes - Definition with Examples", www.splashlearn.com, Retrieved 6-5-2020. Edited.
- ^ أ ب ت ث رجائي سميح العصار، جواد يونس أبو هليل،محمد زهير أبو صبيح (2013)، مدخل إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_ مكتبة العبيكان، صفحة 80-90، جزء الأول. بتصرّف.
- ↑ "Surface Area of a Cylinder", www.varsitytutors.com, Retrieved 6-5-2020. Edited.
- ↑ "Cuboid", www.mathworld.wolfram.com, Retrieved 9-12-2017. Edited.
- ↑ "Surface Area of a Pyramid", www.varsitytutors.com, Retrieved 6-5-2020. Edited.
- ↑ "Surface Area of a Sphere", www.onlinemathlearning.com, Retrieved 6-5-2020. Edited.
- ↑ "Area Of Shapes", byjus.com, Retrieved 6-5-2020. Edited.
- ↑ "Surface Area of a Prism", www.varsitytutors.com, Retrieved 6-5-2020. Edited.
- ↑ "Irregular Polygons", technologyuk, Retrieved 30/8/2021. Edited.
- ^ أ ب "How To Calculate The Area of an Irregular Shape", sciencing, Retrieved 30/8/2021. Edited.
- ↑ "Area of Irregular Polygons", mathsisfun, Retrieved 3/9/2021. Edited.
- ↑ "How to Calculate an Area in AutoCAD", tutorial45, Retrieved 3/9/2021. Edited.
- ↑ "Finding areas by integration", www.mathcentre.ac.uk, Retrieved 16/1/2017. Edited.