محتويات
- ١ مفهوم مساحة المربع
- ٢ كيفية حساب مساحة المربع
- ٣ مسائل متنوعة على حساب مساحة المربع
- ٣.١ احسب مساحة صورة مربعة الشكل طول ضلعها يساوي 8 (سم)
- ٣.٢ احسب مساحة موقف سيارات مربع الشكل إذا كان طول قطره يساوي 40 (م)
- ٣.٣ حديقة مربعة الشكل إذا كان محيطها يساوي 40 (م) أوجد مساحتها
- ٣.٤ احسب مساحة ممحاة مربعة الشكل بوحدة (دسم2) إذا كان طول ضلعها يساوي 30 (سم)
- ٣.٥ احسب مساحة مربع إذا كان طول قطره يساوي 2√ م؛ أي الجذر التربيعي للرقم 2
- ٣.٦ احسب مساحة المربع إذا كان طول ضلعه يساوي نصف مساحته
- ٤ المراجع

مفهوم مساحة المربع
يُقصد بالمساحة (بالإنجليزيّة: Area) الحيز الذي يشغله جسم مسطح أو سطح أي مجسم، كما يُمكن التعبير عن مساحة الشكل بأنه عدد الوحدات المربعة التي تغطي سطح المجسم أو الشكل من الخارج،[١] ويمكن حساب مساحة الأشكال الهندسية بسهولة، حيث يُفيد معرفة المساحة في كثير من التطبيقات الحياتية؛ فمثلًا نحتاج للمساحة عند حساب كمية الطلاء التي نحتاجها لتغطية منطقة معينة، كما نحتاج لمفهوم المساحة في البناء والهندسة والزراعة وغيرها الكثير.[٢]
كيفية حساب مساحة المربع
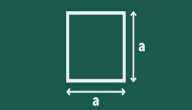
يتم تصنيف المربع على أنه شكل رباعي متساوي الأضلاع، ويتم التعبير عن الحيز الذي يشغل المنطقة المحصورة بين أضلاع المربع بمصطلح مساحة المربع (بالإنجليزيّة: Area of square)،[٣] ولإيجاد مساحة المربع لا بد من معرفة طول ضلعه كما يمكن معرفة مساحة المربع من خلال معرفة طول قطره أيضًا؛ وطول القطر هو الخط المستقيم الممتد من أحد زوايا المربع إلى الزاوية المقابلة لها، ويمكن حساب مساحة المربع كما يأتي:[٤]
مساحة المربع باستخدام طول الضلع
يمكن حساب مساحة المربع باستخدام طول الضلع من خلال التعويض في المعادلة الآتية:
مساحة المربع= طول الضلع * طول الضلع، وبالرموز A= S * S = S^2، وتمثل الرموز ما يأتي:[٥]
- A: مساحة المربع
- S: طول الضلع.
ويجدر الانتباه إلى أن وحدة قياس المساحة هي مربع الوحدة؛ ففي حال حساب مساحة مربع طول ضلعه مُقاسًا بوحدة سم (سنتيمتر) فإن مساحة المربع هنا تكون بوحدة سم2 (سنتيمتر مربع)، بينما في حال حساب طول الضلع بوحدة م (متر) فإن مساحة المربع تكون بوحدة م2 (متر مربع) وهكذا.[٦]
مساحة المربع باستخدام طول القطر
يمكن حساب مساحة المربع عند معرفة قطره؛ فبما أن جميع زوايا المربع قائمة يمكننا الاستعانة بنظرية فيثاغورس الشهيرة (بالإنجليزيّة: Pythagoras Theorem)، والتي تنص على أن مجموع مربع طول ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر، ومن خلال التعويض في هذه المعادلة يمكننا حساب طول ضلع المربع، والذي يساعدنا في حساب مساحة المربع بسهولة كما أسلفنا سابقًا، ولكن بعد اختصار المعادلات تلخص لنا بأنه يمكن حساب مساحة المربع باستخدام طول القطر، ويتم ذلك من خلال التعويض في المعادلة الآتية: [٧]
مساحة المربع = 1/2 * طول القطر * طول القطر، وبالرموز؛ A= 1/2 * D^2، وتمثل الرموز ما يأتي:[٧]
- A: مساحة المربع.
- D: طول القطر.
مسائل متنوعة على حساب مساحة المربع
فيما يأتي مجموعة من المسائل المتنوعة لحساب مساحة المربع:
احسب مساحة صورة مربعة الشكل طول ضلعها يساوي 8 (سم)
الحل:
- يتم التعويض في قانون حساب مساحة المربع باستخدام طول الضلع.
- مساحة المربع= طول الضلع * طول الضلع
- مساحة المربع= 8 (سم) * 8 (سم)
- مساحة الصورة= 64 (سم2)
احسب مساحة موقف سيارات مربع الشكل إذا كان طول قطره يساوي 40 (م)
الحل:
- يتم التعويض في معادلة مساحة المربع باستخدام طول قطره.
- مساحة المربع= 1/2 * طول القطر * طول القطر
- مساحة المربع = 1/2 * 40 (م) * 40 (م)
- مساحة المربع = 800 (م2)
حديقة مربعة الشكل إذا كان محيطها يساوي 40 (م) أوجد مساحتها
الحل:
- يجب إيجاد طول ضلع الحديقة أولًا ليتم حساب مساحتها.
- لإيجاد طول ضلع المربع يتم التعويض في معادلة محيط المربع والتي تربط بين محيط المربع وطول ضلعه.
- محيط المربع= طول الضلع * عدد الأضلاع؛ أي أن محيط المربع = 4 * طول الضلع.
- 40 م= 4 * طول الضلع.
- يتم قسمة طرفيّ المعادلة على 4.
- 40/4 م= 4/4 * طول الضلع.
- طول ضلع مربع الحديقة= 10 (م).
- لحساب مساحة الحديقة يتم التعويض في معادلة مساحة المربع باستخدام طول الضلع.
- مساحة المربع = طول الضلع * طول الضلع.
- مساحة المربع= 10 (م) * 10 (م).
- مساحة الحديقة= 100 (م2).
احسب مساحة ممحاة مربعة الشكل بوحدة (دسم2) إذا كان طول ضلعها يساوي 30 (سم)
الحل: يجب الانتباه أولًا إلى اختلاف وحدة القياس بين طول ضلع المربع ومساحته، ويمكن إيجاد الحل بطريقتين:
- الطريقة الأولى: يتم تحويل وحدة قياس طول الضلع إلى وحدة القياس المطلوبة وهي (دسم)، ثم يتم التعويض في معادلة مساحة المربع من خلال طول الضلع:
- 30 (سم)= 3 (دسم)؛ وعند التحويل من وحدة (سم) إلى (دسم) نقسم العدد على 10.
- مساحة المربع = طول الضلع * طول الضلع.
- مساحة المربع = 3 (دسم) * 3 (دسم).
- مساحة الممحاة = 9 (دسم2).
- الطريقة الثانية: يتم التعويض في معادلة مساحة المربع من خلال طول الضلع لإيجاد المساحة بوحدة قياس (سم2)، وبعد ذلك يتم تحويل وحدة القياس إلى (دسم2):
- مساحة المربع= طول الضلع * طول الضلع.
- مساحة المربع= 30 سم * 30 سم.
- مساحة الممحاة= 900 (سم2).
- 900 (شم2) = 9 (دسم2)؛ عند التحويل من (سم2) إلى (دسم2) نقسم العدد على 100.
احسب مساحة مربع إذا كان طول قطره يساوي 2√ م؛ أي الجذر التربيعي للرقم 2
الحل:
- يتم التعويض في معادلة مساحة المربع من خلال طول قطره.
- مساحة المربع= 1/2 * طول القطر * طول القطر.
- مساحة المربع= 1/2 * 2√ (م) * 2√ (م).
- مساحة المربع= 1 (م2)؛ ( وذلك لأن 2√ * 2√ = 2√ ^ 2 = 2).
احسب مساحة المربع إذا كان طول ضلعه يساوي نصف مساحته
الحل:
- يتم التعويض في معادلة مساحة المربع من خلال طول ضلعه.
- مساحة المربع= طول الضلع * طول الضلع.
- مساحة المربع= (1/2 × مساحة المربع) × (1/2 × مساحة المربع)؛ وتم تعويض 1/2 مساحة المربع بدلًا عن طول الضلع لأنهما متساويان حسب معطيات السؤال.
- مساحة المربع= 1/4× مساحة المربع^2؛ تم تجميع المترادفات معًا.
- من خلال قسمة طرفيّ المعادلة على مساحة المربع ينتج أن مساحة المربع= 4
المراجع
- ↑ "Area - Definition with Examples", splashlearn, Retrieved 20/8/2021. Edited.
- ↑ "Important Surface Area Formulas", engineeringfeed, Retrieved 20/8/2021. Edited.
- ↑ "Area of Square Formula", toppr, Retrieved 20/8/2021. Edited.
- ↑ "Area of Square Using Diagonal", vedantu, Retrieved 20/8/2021. Edited.
- ↑ "Area of Square", cuemath, Retrieved 20/8/2021. Edited.
- ↑ "Area", math-only-math, Retrieved 20/8/2021. Edited.
- ^ أ ب "Area of Square Using Diagonal", vedantu, Retrieved 20/8/2021. Edited.