محتويات

ارتفاع شبه المنحرف
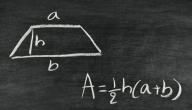
يُعبّر ارتفاع شبه المنحرف عن المسافة العمودية الواصلة بين القاعدة العلوية والسفلية لشبه المنحرف، حيث إنّ شبه المنحرف (بالإنجليزية: Trapezoid) هو أحد الأشكال الهندسية الذي يتكون من 4 أضلاع، اثنان منها متوازيان، يُطلق عليهما اسم القاعدة السفلية، والقاعدة العلوية، أمّا الضلعان المتبقيان غير المتوازيين فيُطلق عليهما اسم الساقين.[١]
حساب ارتفاع شبه المنحرف
يُمكن حساب ارتفاع شبه المنحرف بأكثر من طريقة، وفيما يأتي توضيح لذلك:
حساب ارتفاع شبه المنحرف بمعرفة طول القاعدتين
لحساب ارتفاع شبه المنحرف عند معرفة أطوال القاعدتين لا بدّ من استخدام قانون لمساحة شبه المنحرف وإعادة ترتيب المتغيرات، كالآتي:[٢]
- مساحة شبه المنحرف= ½×(القاعدة الأولى + القاعدة الثانية)×الارتفاع
- بإعادة ترتيب المتغيرات في المعادلة السابقة يُمكن الحصول على قانون حساب ارتفاع شبه المنحرف وهو كالآتي:
ارتفاع شبه المنحرف= 2× (مساحة شبه المنحرف) ÷ (القاعدة الأولى+القاعدة الثانية)
وبالرموز: ع = (2×م) ÷ (أ+ب)
حيث إنّ:
- ع: ارتفاع شبه المنحرف.
- م: مساحة شبه المنحرف.
- أ، ب: طول قاعدتي شبه المنحرف العلوية والسفلية، وهما الضلعان المتوازيان فيه.
حساب ارتفاع شبه المنحرف بمعرفة الزاوية المحصورة بين الساق والقاعدة السفلية
يمكن كذلك حساب الارتفاع عن طريق استخدام القانون الآتي:[٣]
ارتفاع شبه المنحرف= طول إحدى ساقي شبه المنحرف× جا (الزاوية المحصورة بين الساق والقاعدة السفلية)
وبالرموز: ع = جـ× جا(س)
حيث إنّ:
- ع: ارتفاع شبه المنحرف.
- جـ: طول إحدى ساقي شبه المنحرف.
- س: الزاوية المحصورة بين الساق (جـ)، والقاعدة السفلية.
أمثلة على حساب ارتفاع شبه المنحرف
فيما يأتي بعض الأمثلة المحلولة على حساب ارتفاع شبه المنحرف:
المثال الأول: إذا كان هناك شبه منحرف طول قاعدته الكبرى=12سم، وقاعدته الصغرى =4 سم، ومساحته هي 128سم، جد ارتفاعه. [٢]
الحل:
- ارتفاع شبه المنحرف= 2× (مساحة شبه المنحرف) ÷ (القاعدة الأولى+القاعدة الثانية)
- الارتفاع= 2×128 ÷ (12+4) = 16سم.
المثال الثاني: جد ارتفاع شبه المنحرف (أب ج د) إذا كان طول الضلع الجانبي (أج)=13م، وطول (ج و)= 5م، حيث تقع النقطة (و) على القاعدة (ج د) عند نهاية المستقيم العمودي الواصل بين الزاوية (أ) والقاعدة.[٤]
الحل:
- يمكن حساب الارتفاع وهو طول القطعة (أو) عن طريق تطبيق نظرية فيثاغورس على المثلث (أوج) قائم الزاوية في (و)، وعليه:
- (أج)²=(أو)²+(ج و)²
- ومنه (13)²=(أو)²+(5)²، ومنه أو=12سم.
المثال الثالث: إذا كان هناك شبه منحرف طول قاعدته السفلية=15سم، والقاعدة العلوية قياسها=12.8سم، ومساحته هي 97.3سم²، جد ارتفاعه.[٥]
الحل:
- ارتفاع شبه المنحرف= 2× (مساحة شبه المنحرف) ÷ (القاعدة الأولى+القاعدة الثانية)
- الارتفاع= 2×97.3 ÷ (12.8+15)=7سم.
المثال الرابع: جد ارتفاع شبه المنحرف إذا كانت مساحته=77سم²، وطول القاعدة العلوية=8سم، والقاعدة السفلية=14سم.[٦]
الحل:
- ارتفاع شبه المنحرف= 2× (مساحة شبه المنحرف) ÷ (القاعدة الأولى+القاعدة الثانية)
- الارتفاع= 2×77 ÷ (8+14)=7سم.
المراجع
- ↑ Maitreyee (4-2-2018), "How to Find the Altitude of a Trapezoid"، www.study.com, Retrieved 12-5-2019. Edited.
- ^ أ ب Damon Verial (13-3-2018), "How to Find the Height of a Trapezoid"، www.sciencing.com, Retrieved 12-5-2019. Edited.
- ↑ "Properties of a Trapezoid", www.moomoomath.com, Retrieved 2-12-2019. Edited.
- ↑ "Example Questions", www.varsitytutors.com, Retrieved 24-2-2020. Edited.
- ↑ "how do you find the height of a trapezoid if you know the area and bases?", virtualnerd.com, Retrieved 24-2-2020. Edited.
- ↑ "Area of Trapezoids", www.murrieta.k12.ca.us, Retrieved 24-2-2020. Edited.