محتويات

قوانين علم حساب المثلثات في المثلث قائم الزاوية
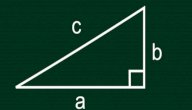
يُعتبر المثلث قائم الزاوية أكثر أنواع المثلثات أهمية في علم حساب المُثلث الذي لا يقتصر فقط على حساب المثلثات قائمة الزاوية، ويُرمز في المثلث القائم للزاوية القائمة ذات القياس 90 درجة بِمربع صغير على الزاوية، في حين يُرمز لإحدى الزاويتين الأُخريتين بالرمز س، ويحتوي هذ المُثلث على ثلاثة أضلاع وهي:[١]
- الضلع المُجاور
(بالإنجليزية: Adjacent) هو الضلع المُجاور أو القريب من الزاوية س.
- الضلع المُقابل
(بالإنجليزية: Opposite) هو الضلع الذي يقُابل أو يُواجه الزاوية س.
- الوتر
(بالإنجليزية: Hypotenuse) هو الضلع الأطول في المُثلث.
المتطابقات المثلثية الأساسية
ومن أهم الاقترانات أو النسب المثلثية للمثلث قائم الزاوية في علم حساب المثلثات ما يلي:[١]
- الجيب (بالإنجليزية: sine): ويُرمز له بالرمز (جا): وقانونه هو للزاوية (س) في المثلث قائم الزاوية:
- جاس= الضلع المُقابل للزاوية س÷ وتر المثلث.
- جيب التمام (بالإنجليزية: cosine)، ويُرمز له بالرمز (جتا): وقانونه للزاوية (س) في المثلث قائم الزاوية هو:
- جتا س= الضلع المجاور للزاوية س÷ وتر المثلث.
- الظل (بالإنجليزية: tangent)، ويُرمز له بالرمز (ظا)، وقانونه للزاوية (س) في المثلث قائم الزاوية هو:
- ظا س= الضلع المقابل للزاوية س÷ الضلع المجاور للزاوية س= جا(س)/ جتا (س).
- القاطع (بالإنجليزية: secant): ويُرمز له بالرمز (قا)، وقانونه للزاوية (س) في المثلث قائم الزاوية هو:
- قا س= وتر المثلث ÷ الضلع المجاور للزاوية س= 1÷ جتا س .
- قاطع التمام (بالإنجليزية: cosecant): ويُرمز له بالرمز (قتا)، وقانونه للزاوية (س) في المثلث قائم الزاوية هو:
- قتا س= وتر المثلث ÷ الضلع المقابل للزاوية س= 1÷ جا س .
- ظل التمام (بالإنجليزية: cotangent): ويُرمز له بالرمز (ظتا)، وقانونه للزاوية (س) في المثلث قائم الزاوية هو:
- ظتا س= الضلع المجاور للزاوية س÷ الضلع المقابل للزاوية س=1÷ ظا س= جتا (س)/ جا (س).
مُتطابقات فيثاغورس
تشمل متطابقات فيثاغورس (بالإنجليزية: Pythagorean identities) ما يلي:[٢]
- جتا² س+ جا² س= 1
- قا² س- ظا² س= 1
- قتا² س- ظتا² س= 1
متطابقات ضعف الزاوية
تشمل متطابقات ضعف الزاوية (بالإنجليزية: Double Angle Identities) ما يلي:[٢]
- جا 2س= 2 جاس جتاس.
- جتا 2س= جتا² س- جا² س.
- ظا 2س = 2 ظاس/ (1-ظا² س)
- ظتا 2س=(ظتا²س-1)/2 ظتاس.
متطابقات نصف الزاوية
متطابقات نصف الزاوية (بالإنجليزية: Half Angle Identities)، وهي:[١]
- جا (س/2)=± ((1-جتا س)/2)√
- جتا (س/2)=± ((1+جتا س)/2)√
- ظا (س/2)=± ((1-جتا س)/(1+جتا س))√= جاس/(1+جتا س)= 1-جتا س/ جا س= قتا س-ظتا س.
- ظتا (س/2)=± ((1+جتا س)/(1-جتا س))√= جاس/(1-جتا س)= 1+جتا س/ جا س= قتا س+ظتا س.
مُتطابقات الجمع والطرح
تشمل متطابقات الجمع والطرح (بالإنجليزية: Sum and Difference identities) ما يلي:[٢]
- جا (س±ص) = جا (س) جتا (ص) ± جتا (س) جا (ص).
- جتا (س+ص) = جتا (س) جتا (ص) - جا (س) جا (ص).
- جتا (س-ص) = جتا (س) جتا (ص) + جا (س) جا (ص).
- ظا (س+ص) = ظا (س) + ظا (س)/ (1-(ظا س ظا ص).
- ظا (س-ص) = ظا (س) - ظا (س)/ (1+(ظا س ظا ص).
متطابقات الضرب والجمع
تشمل متطابقات الضرب والجمع (بالإنجليزية: Product-to-Sum identities) ما يلي:[٣]
- جاس جا ص= ½ [جتا(س-ص)- جتا (س+ص)]
- جتاس جتا ص= ½ [جتا(س-ص)+ جتا (س+ص)]
- جاس جتا ص= ½ [جا(س+ص)+ جا (س-ص)]
- جتاس جا ص= ½ [جا(س+ص)- جا (س-ص)]
متطابقات عكس الزاوية
تشمل متطابقات عكس الزاوية (بالإنجليزية: Opposite Angle Identities) ما يلي:[١]
- جا (-س)= - جا س.
- جتا (-س)= جتا س.
- ظا (-س)= - ظا (س).
متطابقات الزاويا المتتامة
تشمل متطابقات الزوايا المتتامة (بالإنجليزية: Complementary Angle Identities) ما يلي:[٤]
- جا (90-س)= جتا س.
- جتا (90-س)= جا س.
- ظا (90-س)= ظتا س.
- ظتا (90-س)= ظا س.
- قا (90-س)= قتا س.
- قتا (90-س)= قا س.
متطابقات الزاويا المتكاملة
تشمل متطابقات الزوايا المتكاملة (بالإنجليزية: Supplementary Angle Identities) ما يلي:[٥]
- جا س= جا (180-س).
- جتا س= - جتا (180-س).
- ظا س= - ظا (180-س).
قانون الجيب وقانون جيب تمام الزاوية
يعتبر قانونا الجيب وجيب تمام الزاوية من المتطابقات المثلثية التي تنطبق على جميع المثلثات وليس على المثلثات قائمة الزاوية فقط، وهما كما يلي:[٦]
قانون الجيب
يصاغ قانون الجيب على الشكل الآتي:[٦]
(أ/جا أَ)=(ب/جا بَ)=(جـ/جا جـَ)
حيث إنَّ:
- (أ، ب، ج): هي أطوال أضلاع المثلث
- (أَ، بَ، جَ): هي الزوايا المقابلة على الترتيب لهذه الأضلاع.
قانون جيب تمام الزاوية
- أ² = ب²+جـ² -(2×ب×جـ×جتا أَ)، حيث إن: (أَ) هي الزاوية المحصورة بين الضلعين (جـ) و(ب)، والمقابلة للضلع أ.
- ب²= أ²+جـ² - (2×أ×جـ×جتا بَ)، حيث إن: (بَ) هي الزاوية المحصورة بين الضلعين (أ) و(جـ)، والمقابلة للضلع ب.
- جـ²= أ²+ب² - (2 ×أ×ب×جتا جـَ)، حيث إن: (جـَ) هي الزاوية المحصورة بين الضلعين (أ) و(ب)، والمقابلة للضلع جـ.
أمثلة متنوعة على حساب المثلثات
- المثال الأول: في مُثلث قائم الزاوية، إذا كان طول الوتر يُساوي 4.9سم، وكان طول الضلع المقابل للزاوية θ يُساوي 2.8سم، أما طول الضلع المجاور لهذه الزاوية فهو 4سم، فإذا كان قياس الزاوية θ يُساوي 35، فما هو جيب هذه الزاوية؟[١]
- الحل:
- جا س= الضلع المُقابل للزاوية θ÷ وتر المثلث
- جا 35= 2.8÷ 4.9= 0.57.
- المثال الثاني: في مُثلث قائم الزاوية، إذا كان طول الوتر يُساوي 25سم، وكان طول الضلع المقابل للزاوية س يُساوي 24سم، أما طول الضلع المجاور لهذه الزاوية فهو 7سم، فما هو جيب، وجيب تمام، وظل هذه الزاوية؟[٧]
- الحل:
- جا س= الضلع المُقابل للزاوية س÷ وتر المثلث= 24÷ 25= 0.96.
- جتا س= الضلع المجاور للزاوية س÷ وتر المثلث=7÷ 25= 0.28.
- ظا س= الضلع المجاور للزاوية س÷ الضلع المُقابل للزاوية= 24÷7= 3.42.
- المثال الثالث: في مُثلث قائم الزاوية إذا كان جا س= 0.4، جتا س= 0.2، جد قيمة ظا س.[٧]
- الحل:
- ظا س= جاس/ جتا س= 0.4/0.2= 2.
- المثال الرابع: بسّط التعابير الآتية إلى أبسط صورة:[٧]جا (2س). قا(س)+ 2 جا (-س).
- (جا 15 +جتا 15)².
- الحل:جا (2س). قا(س)+ 2 جا (-س)
- جا (2س)= 2.جا س.جتاس
- قا(س)= 1/جتا س.
- 2 جا (-س)= - 2جا س.
- بضرب الصيغ السابقة ببعضها ينتج أن: (2×جا س×جتاس) × (1/جتا س) + -2×جا س= 2×جاس - 2×جاس= 0.
- بفك الأقواس ينتج أن: (جا² 15+جتا² 15) + (2×جا 15×جتا 15).
- (جا² 15+جتا² 15)= 1.
- (2×جا 15×جتا 15)= جا 2س= جا 30= 0.5.
- بتجميع القيم السابقة ينتج أن:
- (جا 15 +جتا 15)²= 1+0.5=1.5.
- المثال الخامس: إذا كان جتا س= 4/5، جد قيمة جا 2س.
- الحل:
- جا 2س= 2 جاس جتاس، ولحساب قيمة جا س، يمكن تطبيق نظرية فيثاغورس، كما يلي:
- جتا س= الضلع المجاور للزاوية س/ وتر المثلث= 4/5، ومنه الضلع المجاور للزاوية س=4، والوتر= 5، وبتطبيق نظرية فيثاغور ينتج أن: الوتر²=الضلع الأول²+الضلع الثاني²، ومنه: 5²=4²+الضلع الثاني²، وبترتيب المعادلة وأخذ الجذر التربيعي للطرفين ينتج أن: الضلع الثاني وهو المقابل للزاوية س= 3.
- جا س= الضلع المقابل للزاوية س/الوتر= 3/5.
- بتطبيق ذلك على القانون أعلاه: جا 2س= 2 جاس جتاس، ينتج أن جا 2س= 2× 3/5 × 4/5= 24/25.
- المثال السادس: إذا كان طول الضلع أب، أو القاعدة في المثلث أب ج يساوي ج، وطول الضلع أج يساوي 3سم، والضلع ب ج يساوي أ، وقياس الزاوية ج= 85 درجة، وقياس الزاوية أ = 35 درجة، ما هو قياس الضلعين أ، ج، والزاوية ب.[٨]
- الحل:
- قياس الزاوية ب= 180-(أ+ج)= 180- (35+85)= 60 درجة ؛لأن مجموع زوايا المثلث يساوي 180 درجة.
- بتطبيق قانون الجيب:
- (أ/جا أَ)= (ب/جا بَ)= (جـ/جا جـَ): ينتج أن:
- 3/جا60= أ/جا 35، ومنه: أ= 1.99سم.
- 3/جا60= ج/جا 85، ومنه: ج= 3.45سم.
- المثال السابع: جد قيمة ما يلي:[٩]
- جتا 105، باستخدام حقيقة: 105=60+45.
- جا 60 جتا 30 + جتا 60 جا 30.
- الحل:جتا 105، عند التعبير عنه كمجموع زاويتين باستخدام: جتا (س+ص) = جتا (س) جتا (ص) - جا (س) جا (ص)، هو:
- جتا 105= جتا (60+45)= جتا (60) جتا (45) - جا (60) جا (45)= 0.5 × 2/2√ - 2 /3√× 2/2√ = 2√-6√/4.
- جا 60 جتا 30 + جتا 60 جا 30، يمكن حل هذه المسألة ببساطة عن طريق الاستفادة من صيغة: جا (س±ص) = جا (س) جتا (ص) ± جتا (س) جا (ص)، لينتج ما يلي:
- جا 60 جتا 30 + جتا 60 جا 30 = جا (60+30)= جا (90) = 1.
- المثال الثامن: إذا كان جا أ= 0.1، جتا ب= 0.1، جد قيمة جا (أ- 2ب)، علماً أن: ب تقع في الربع الرابع، وأ تقع في الربع الأول.[٩]
- الحل:
- جا (أ- 2ب)، يمكن كتابتها وفق الصيغة: جا (س±ص) = جا (س) جتا (ص) ± جتا (س) جا (ص)، على شكل:
- جا (أ- 2ب)= جا (أ) جتا (2ب) - جتا (أ) جا (2ب)، أما جتا 2ب، جا 2ب، فيمكن التعبير عنهما باستخدام الصيغتين: جا 2س، جتا 2س= جتا² س- جا² س، جا 2س= 2 جا س جتا س، على شكل:
- جتا 2ب = جتا² ب- جا² ب.
- جا 2ب = 2 جاب جتاب.
- جا² ب = 1- جتا² ب= 1- 0.1²= 0.99، ومنه: جا ب= 0.995-؛ لأن ب تقع في الربع الرابع وفق معطيات السؤال.
- جتا² أ = 1- جا² أ= 1- 0.1²، ومنه: جتا أ= 0.995؛ لأن أ تقع في الربع الأول وفق معطيات السؤال.
- بتعويض ما سبق ينتج أن:
- جا (أ- 2ب)= جا أ× (جتا² ب- جا² ب) - جتا أ× 2 × جاب ×جتاب= 0.1× (0.1²- ²(0.995-))- 0.995× 2 × -0.995 × 0.1= 0.1.
- المثال التاسع: إذا كانت الزاوية θ في ربع دائرة ما تساوي جا س=- 24/25، جد قيمة جتا س باستخدام متطابقات فيثاغورس؟[١٠]
- الحل:
- باستخدام متطابقات فيثاغورس: فإن جتا² س+ جا² س= 1
- جتا² س+ (- 24/25)² = 1
- جتا² س= 1 - (- 24/25)²
- جتا² س√= 49/625√
- جتا س= 7/25
- الحل:
- المثال العاشر: جد جتا الزاوية 165ْ باستخدام متطابقات نصف الزاوية.[١١]
- الحل:
- باستخدام متطابقة نصف الزاوية الآتية: جتا (س/2)= ± ((1+جتا س)/2)√
- جتا 165ْ= جتا 330ْ/2، حيث أن س/2 تساوي 165، ومنها، س = 330 وهي ضعف 165.
- جتا 165ْ= (1+جتا330ْ) /2 √
- جتا 165ْ= (1+ (3/2√-)) /2 √-
- جتا 165ْ= (2 +3√)/4 √-
- جتا 165ْ= (3√+2)√ /2-
- المثال الحادي عشر: جد ناتج المعادلة الآتية باستخدام متطابقات الزوايا المتتامة، أ=جا 37ْ جتا 53ْ+جا 53ْ جتا 37ْ.[١٢]
- الحل: باستخدام متطابقات الزوايا المتتامة: جا 53ْ = جتا(90ْ - 53ْ) = جتا 37ْ.
- جتا 53ْ = جا(90ْ - 53ْ) = جا 37ْ
- وبالتالي، أ= جا² 37 + جتا² 37 = 1
فيديو عن كيفية حساب مساحة المثلث
للتعرف على كيفية حساب مساحة المثلث شاهد هذا الفيديو.
المراجع
- ^ أ ب ت ث ج "trigonometry", www.mathsisfun.com, Retrieved 5-3-2019. Edited.
- ^ أ ب ت "Trigonometry", byjus.com, Retrieved 9-4-2020. Edited.
- ↑ " Table of Trigonometric Identities", www.sosmath.com, Retrieved 9-4-2020. Edited.
- ↑ "Trigonometric Identities", byjus.com, Retrieved 9-4-2020. Edited.
- ↑ "Trigonometric identities of other angles", www.sangakoo.com, Retrieved 9-4-2020. Edited.
- ^ أ ب ت "The sine rule and cosine rule", www.mathcentre.ac.uk, Retrieved 9-4-2020. Edited.
- ^ أ ب ت "Sin, Cos, Tan", www.varsitytutors.com, Retrieved 9-4-2020. Edited.
- ↑ "Sine and Cosine Rules - Trigonometry", mathematics.laerd.com, Retrieved 9-4-2020. Edited.
- ^ أ ب "Identities with Angle Sums", www.varsitytutors.com, Retrieved 9-4-2020. Edited.
- ↑ "pythagorean-identity-review", khanacademy, Retrieved 6/10/2021.
- ↑ "double-angle-and-half-angle-identities", cliffsnotes, Retrieved 2/10/2021.
- ↑ "trigonometric-ratios-of-complementary-angles", cuemath, Retrieved 2/10/2021.