محتويات

تعريف متوازي المستطيلات
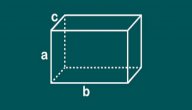
يمكن تعريف متوازي المستطيلات (بالإنجليزية: Cuboid) بأنه أحد المُجسّمات الهندسية الثلاثية الأبعاد؛ أي له طول، وعرض، وارتفاع، وهو يشبه في شكله شكل الصندوق، ويُعتبر بشكل عام حالة خاصة من المنشور.[١][٢][٣]
أجزاء متوازي المستطيلات
يتكون متوازي المستطيلات من الأجزاء التالية:
- الوجوه
الوجوه (وبالإنجليزية: Faces) لمتوازي المستطيلات ستة أسطح على شكل مستطيلات، تُعرف باسم وجوه متوازي المستطيلات.
- الأحرف
الأحرف (وبالإنجليزية: Edge) هي حوافّه المكوّنة للأسطح ويمكن تعريفها بشكل آخر بأنها الخطوط المستقيمة الواصلة بين كل رأسين متجاورين في متوازي المستطيلات.
- الرؤوس
الرؤوس (وبالإنجليزية: Vertices) هي النقاط أو الزوايا التي تلتقي عندها عادة ثلاثة أحرف لمتوازي المستطيلات، وجميعها قائمة.
خصائص متوازي المستطيلات
يمتاز متوازي المستطيلات إضافة لما ذُكر في التعريف السابق بمجموعة من الخصائص، وهي:[٤]
- كلّ زوج من الأوجه المُتقابِلة في متوازي المستطيلات متوازية ومتطابقة تماماً.
- لمتوازي المستطيلات ستة وجوه، وثمانية رؤوس، واثنا عشر حرفاً.
- الحواف المتقابلة لمتوازي المستطيلات متوازية.
يجدر بالذكر هنا أنه إذا تساوى الطول، والعرض، والارتفاع في طولهما فإن متوازي المستطيلات يُعرف وقتها باسم المكعّب (بالإنجليزية: Cube).[٣]
مساحة متوازي المستطيلات
يمكن حساب مساحة متوازي المستطيلات باستخدام القوانين الآتية:
قانون مساحة متوازي المستطيلات
يمكن حساب مساحة متوازي المستطيلات باستخدام القانون الآتي:[٥][٦]
- المساحة الكلية متوازي المستطيلات= 2× (الطول×العرض+الطول×الارتفاع+العرض×الارتفاع)، وبالرموز: م=2× (س×ص+س×ع+ص×ع)؛ حيث:
- م: مساحة متوازي المستطيلات.
- س: طول متوازي المستطيلات.
- ص: عرض متوازي المستطيلات.
- ع: ارتفاع متوازي المستطيلات.
- أما المساحة الجانبية لمتوازي المستطيلات، وهي مجموع مساحة كافة الأوجه عدا القاعدتين، فتساوي: 2× (الطول+العرض) ×الارتفاع، وبالرموز: المساحة الجانبية لمتوازي المستطيلات=2× (س+ص) ×ع؛ حيث:
- س: طول متوازي المستطيلات.
- ص: عرض متوازي المستطيلات.
- ع: ارتفاع متوازي المستطيلات.
- وبصورة أخرى: المساحة الكلية لمتوازي المستطيلات= المساحة الجانبية+ مساحة القاعدتين.
ولتوضيح ما سبق فإن متوازي المستطيلات يعتبر شكلاً ذا أوجه متعددة، ولإيجاد مساحته يجب إيجاد مجموع مساحات أوجهه الستة كاملة، وبالتالي فإن مساحة متوازي المستطيلات= مساحة الوجه الأول+ مساحة الوجه الثاني+ مساحة الوجه الثالث+ مساحة الوجه الرابع+ مساحة الوجه الخامس+ مساحة الوجه السادس.[٧]
وبما أن كل زوج من الأوجه متطابق؛ فإن المساحة= 2×مساحة الوجه الأول (مساحة القاعدتين) + 2×مساحة الوجه الثاني (مساحة أول وجهين جانبيين) +2×مساحة الوجه الثالث (مساحة ثاني وجهين جانبيين) = 2×الطول×العرض (مساحة القاعديتن) + 2×العرض× الارتفاع (مساحة أول وجهين جانبيين) +2×الطول×الارتفاع (مساحة ثاني وجهين جانبيين)، علماً أن مساحة المستطيل=الطول×العرض.[٧]
أمثلة على حساب مساحة متوازي المستطيلات
وفيما يأتي بعض الأمثلة على حساب مساحة متوازي المستطيلات:
حساب المساحة الجانبية لمتوازي المستطيلات
مثال: إذا كان طول قاعدة متوازي مستطيلات 3سم، وعرضها 5سم، أما ارتفاعه فيساوي 4سم، جد مساحته الجانبية.[٥]
الحل: المساحة الجانبية لمتوازي المستطيلات= 2× (الطول+العرض) ×الارتفاع=2× (3+5) ×4=64سم².
حساب المساحة الكلية لمتوازي المستطيلات
المثال الأول: متوازي مستطيلات، طول قاعدته 10م، وعرضها 4م، أما ارتفاعه فيساوي 5م، جد المساحة الكلية لمتوازي المستطيلات.[٨]
الحل: باستخدام القانون: المساحة الكلية متوازي المستطيلات= 2× (الطول×العرض+الطول×الارتفاع+العرض×الارتفاع) =2× (10×4+10×5+4×5)، ومنه المساحة الكلية لمتوازي المستطيلات =220م².
المثال الثاني: إذا كان طول قاعدة صندوق على شكل متوازي مستطيلات 40سم، وعرضها 31سم، أما ارتفاعه فيساوي 12سم، جد مساحته الكلية لتغليفه بالكامل بورق الهدايا.
الحل: باستخدام القانون: المساحة الكلية متوازي المستطيلات= 2× (الطول×العرض+الطول×الارتفاع+العرض×الارتفاع) =2× (40×31+40×12+31×12)، ومنه المساحة الكلية لمتوازي المستطيلات =4,184م².
حجم متوازي المستطيلات
يمكن حساب حجم متوازي المستطيلات باستخدام القوانين الآتية:
قانون حجم متوازي المستطيلات
يمكن حساب حجم متوازي المستطيلات الذي يعبّر عن مقدار الفراغ الموجود بداخله عن طريق استخدام العلاقة الآتية:[١]
حجم متوازي المستطيلات= الطول×العرض×الارتفاع
وبالرموز: ح= س×ص×ع
حيث:
- ح: حجم متوازي المستطيلات.
- س: طول متوازي المستطيلات.
- ص: عرض متوازي المستطيلات.
- ع: ارتفاع متوازي المستطيلات.
أمثلة على حساب حجم متوازي المستطيلات
المثال الأول: دفتر صغير على شكل متوازي مستطيلات، طول قاعدته 6سم، وعرضها 4سم، أما ارتفاعه فيساوي 1سم، فجد كم يلزم من الصفحات لتعبئته.[١]
الحل: باستخدام قانون حجم متوازي المستطيلات= الطول×العرض×الارتفاع=6×4×1=24سم³، وعليه فهو يحتاج 24سم³ من الصفحات لتعبئته.
المثال الثاني: جد حجم الشوكولاتة الموجودة داخل علبة على شكل متوازي مستطيلات، إذا كان طول قاعدتها 12سم، وعرضها 5سم، أما ارتفاعها 2.4سم.[١]
الحل: باستخدام قانون حجم متوازي المستطيلات= الطول×العرض×الارتفاع=12×5×2.4=144سم³، وعليه فإن حجم الشوكولاتة الموجودة داخل العلبة=144سم³.
أقطار متوازي المستطيلات
لمتوازي المستطيلات نوعان مختلفان من الأقطار، هما:[٢][١٠]
- أقطار الوجه: (بالإنجليزية: Face Diagonals) وهي الخطوط المستقيمة الواصلة بين كل زاويتين متقابلتين لأوجه متوازي المستطيلات، ولكل وجه قطران، بمجموع يبلغ اثني عشر قطراً لكامل متوازي المستطيلات، ولحساب طولها يمكن استخدام القانون الآتي:
- طول قطر القاعدتين=الجذر التربيعي لـ (مربع الطول+مربع العرض)، وبالرموز: طول قطر القاعدتين= (س²+ص²) √.
- طول قطر أول وجهين جانيين=الجذر التربيعي لـ (مربع الطول+مربع الارتفاع)، وبالرموز: طول قطر أول وجهين جانيين= (س²+ع²) √.
- طول قطر ثاني وجهين جانيين=الجذر التربيعي لـ (مربع العرض+مربع الارتفاع)، وبالرموز: طول قطر ثاني وجهين جانيين= (ص²+ع²) √؛ حيث:
-
- س: طول متوازي المستطيلات.
- ص: عرض متوازي المستطيلات.
- ع: ارتفاع متوازي المستطيلات.
- أقطار متوازي المستطيلات: (بالإنجليزية: Space Diagonals) وهي عبارة عن القطعة المستقيمة الواصلة بين كلّ رأسين متقابلين في متوازي المستطيلات، ولكل متوازي مستطيلات أربعة أقطار، ويمكن حساب طولها باستخدام القانون الآتي:
- طول قطر متوازي المستطيلات=الجذر التربيعي لـ (مربع الطول+مربع العرض+مربع الارتفاع)، وبالرموز: طول قطر متوازي المستطيلات= (س²+ص²+ع²)√.
فمثلاً لو كان هناك متوازي مستطيلات طول قاعدته 5سم، وعرضها 4سم، وارتفاعه 3سم، فإن طول أقطاره هو: طول قطر متوازي المستطيلات= (س²+ص²+ع²) √= (5²+4²+3²) √=50√سم.[١١]
أمثلة على حساب أقطار متوازي المستطيلات
وفيما يلي بعض الأمثلة على حساب أقطار متوازي المستطيلات:
المثال الأول: بركة سباحة على شكل متوازي مستطيلات، إذا كان طول قاعدتها 13 سم، وعرض قاعدتها 9 سم، وارتفاعها 3 سم، جد طول قطر هذه البركة.
الحل:
- باستخدام قانون طول قطر متوازي المستطيلات= (الطول²+العرض²+الارتفاع²) √
- طول قطر متوازي المستطيلات= (13² + 9² + 3²) √ = 259√ = 16.1 سم.
- وعليه فإنّ طول قطر البركة= 16.1 سم.
المثال الثاني: ما هو طول قطر القاعدتين لمتوازي مستطيلات طول قاعدته 7 سم، وعرض قاعدته 5 سم، وارتفاعه 2 سم؟
الحل:
- باستخدام قانون طول قطر القاعدتين= (الطول²+العرض²) √
- طول قطر القاعدتين= (7²+5²) √= (74) √= 8.6 سم.
- وعليه فإنّ طول قطر القاعدة الأولى= طول قطر القاعدة الثانية= 8.6 سم.
المثال الثالث: ما هو طول قطر كل وجه من أوجه متوازي المستطيلات الذي يبلغ ارتفاعه 5.5 سم، وطول قاعدته 9.6 سم، وعرض قاعدته 7 سم؟
الحل:
- لحساب قطر أول وجهين جانبيين لمتوازي المستطيلات:
- باستخدام قانون طول قطر أول وجهين جانيين= (الطول²+الارتفاع²) √
- طول قطر أول وجهين جانيين = (9.6²+5.5²) √= (122.41) √= 11.06 سم.
- وعليه فإنّ طول قطر أول وجه لمتوازي المستطيلات = طول قطر ثاني وجه لمتوازي المستطيلات= 11.06 سم.
- باستخدام قانون طول قطر ثاني وجهين جانيين= (العرض²+الارتفاع²) √
- طول قطر ثاني وجهين جانيين= (7²+5.5²) √= (79.25) √= 8.9 سم.
- وعليه فإنّ طول قطر ثالث وجه لمتوازي المستطيلات = طول قطر رابع وجه لمتوازي المستطيلات= 8.9 سم.
فيديو عن حجم ومساحة متوازي المستطيلات
للتعرف على هذا الشكل الهندسي تابع الفيديو:[١٢]
المراجع
- ^ أ ب ت ث Alida D, "What is a Cuboid Shape? - Definition, Area & Properties"، study.com, Retrieved 22-3-2020. Edited.
- ^ أ ب "Cuboid | Formulas | Properties of Cuboid", mathsmaker.com, Retrieved 22-3-2020. Edited.
- ^ أ ب رجائي سميح العصار، جواد يونس أبو هليل،محمد زهير أبو صبيح (2013)، مدخل إلى أولمبياد ومسابقات الرياضيات (الطبعة الأولى)، الرياض: جامعة الملك فهد للبترول والمعادن عمادة البحث العلمي_ مكتبة العبيكان، صفحة 85-90، جزء الأول. بتصرّف.
- ↑ "Cube and Cuboid", www.toppr.com, Retrieved 22-3-2020. Edited.
- ^ أ ب "CUBOIDS", www.onlinemath4all.com, Retrieved 22-3-2020. Edited.
- ↑ "Cube and Cuboid", byjus.com, Retrieved 22-3-2020. Edited.
- ^ أ ب "What is a Cuboid Shape? - Definition, Area & Properties", www.study.com, Retrieved 9-12-2017. Edited.
- ↑ "Cuboids, Rectangular Prisms and Cubes", www.mathsisfun.com, Retrieved 9-12-2017. Edited.
- ↑ "What is a Cuboid? - Definition, Shape, Area & Properties", tutors.com, Retrieved 22-3-2020. Edited.
- ↑ "Cuboid", mathworld.wolfram.com, Retrieved 22-3-2020. Edited.
- ↑ "Volume and Surface Area of Cuboid", www.math-only-math.com, Retrieved 22-3-2020. Edited.
- ↑ فيديو عن حجم ومساحة متوازي المستطيلات.