محتويات
- ١ ما هي خصائص متوازي الأضلاع؟
- ٢ حالات خاصة من متوازي الأضلاع
- ٣ أمثلة متنوعة على خصائص متوازي الأضلاع
- ٣.١ حساب قيمة س لزاوية مجهولة في متوازي الأضلاع
- ٣.٢ حساب قيمة زاوية مجهولة في متوازي أضلاع
- ٣.٣ حساب قيمة س وص لزاوية وضلع في متوازي الأضلاع
- ٣.٤ حساب قيمة س وص لزاويتين في متوازي الأضلاع
- ٣.٥ حساب قيمة ثلاث زوايا مجهولة في متوازي الأضلاع
- ٣.٦ حساب قيمة س وص لأضلاع مجهولة في متوازي الأضلاع
- ٣.٧ حساب قيمة س لضلع مجهول في متوازي الأضلاع
- ٤ المراجع

ما هي خصائص متوازي الأضلاع؟
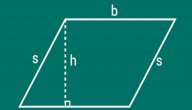
يمكن تعريف متوازي الأضلاع بأنه شكل مسطح ثنائي الأبعاد فيه كل ضلعين متقابلين متساويان، ومتوازيان،[١] ويتميز كذلك بالخصائص الآتية:[٢]
- كل زاويتين متقابلتين متساويتان.
- كل زاويتين متحالفتين (تقعان على ضلع واحد) متكاملتان أي مجموعها 180 درجة.
- إذا كانت إحدى زواياه قائمة، فإن جميع زواياه قوائم كذلك، ويكون في هذه الحالة مستطيلاً، أو مربعاً وهي حالات خاصة من متوازي الأضلاع.
- يتميز متوازي الأضلاع باحتوائه على قطرين، وهي عبارة عن الخطوط المستقيمة التي يمكن رسمها بين أحد رؤوس متوازي الأضلاع، والرأس المقابل له، ويتميز القطران بالخصائص الآتية:[٢]
- كل قطر ينصّف القطر الآخر.
- كل قطر يقسم متوازي الأضلاع إلى مثلثين متطابقين.
حالات خاصة من متوازي الأضلاع
هناك ثلاثة حالات خاصة من متوازي الاضلاع، وهي المستطيل، والمعين، والمربع، وفيما يلي توضيح لكل منها:
المستطيل
بما أن المستطيل هو متوازي أضلاع، فهو يتميز بجميع خصائص متوازي الاضلاع، إلا أن هناك بعض الخصائص التي تميّزه عن متوازي الأضلاع، وهي:[٣]
- جميع زواياه الأربعة قوائم.
- أقطاره متساوية في الطول، وتنصّف زواياه.
المعين
يُعرف المعين بأنه شكل رباعي تكون أضلاعه الأربعة متساوية في الطول، وكل معين هو متوازي أضلاع، وبما أن المعين هو متوازي أضلاع فهو يتّصف بجميع خصائص متوازي الأضلاع، إضافة إلى خصائص أخرى تميّزه عن متوازي الأضلاع، وهي:[٣]
- جميع أضلاعه الأربعة متساوية.
- أقطاره متعامدة على بعضها؛ أي تشكل زاوية قياسها 90 درجة، وتنصّف زواياه.
المربع
يُعرف المربع بأنه متوازي أضلاع يمتلك جميع خصائص المعين والمستطيل، ومن أبرز خصائصه:[٣]
- جميع أطوال أضلاعه متساوية في الطول كالمعين.
- زواياه الأربعة قوائم كالمستطيل.
- أقطاره متساوية في الطول كالمستطيل.
- أقطاره تعامد بعضها كالمعين.
- أقطاره متطابقة كالمستطيل، وتنصف زواياه.
أمثلة متنوعة على خصائص متوازي الأضلاع
وفيما يأتي أمثلة متنوعة على خصائص متوازي الأضلاع:
حساب قيمة س لزاوية مجهولة في متوازي الأضلاع
شكل رباعي أ ب جـ د فيه قياس الزاوية أ: 3س + 9، وقياس الزاوية ب: 5س + 20، وقياس الزاوية جـ: 3س، وقياس الزاوية د: 2س + 6، فما هو قياس الزاوية د؟[٤]
الحل:
- يمكن حل هذا السؤال من خلال معرفة قاعدة أن مجموع زوايا الشكل الرباعي التي تنص على أن مجموع زوايا أي شكل رباعي يساوي 360 درجة.
- وبالتالي فإن 5س+9+5س+20+3س+2س+6= 360.
- 13س+35 =360.
- 13س= 325.
- س= 25.
- وبالتالي فإن قياس الزاوية د: 2×25+6، وتساوي 56 درجة.
حساب قيمة زاوية مجهولة في متوازي أضلاع
متوازي أضلاع د هـ و ي، قاعدته (هـ و) فيه قياس الزاوية د (2س + 12)، وقياس الزاوية هـ (5س)، فما هو قياس الزاوية و؟[٤]
الحل:
- يمكن حل هذا السؤال باستخدام خاصيتين من خصائص متوازي الأضلاع، وهي أن كل زاويتين متحالفتين (تقعان على ضلع واحد) مجموعها 180 درجة، وفي هذا السؤال الزاوية د، والزاوية هـ زاويتان متجاورتان، والخاصية الأخرى أن كل زاويتين متقابلتين متساويتان، وفي هذا السؤال الزاوية د، والزاوية و متقابلتان.
- وعليه: (2س+12) + (5س) = 180 درجة.
- 7س + 12 = 180.
- 7س = 168.
- س= 24.
- وبالتالي فإن قياس الزاوية و يساوي قياس الزاوية د، ويساوي 2 × 24 + 12، ويساوي 60 درجة.
حساب قيمة س وص لزاوية وضلع في متوازي الأضلاع
متوازي أضلاع أ ب جـ د، قاعدته (ب ج) فيه قياس الزاوية أ: (س + 15ص) درجة، وقياس الزاوية جـ 127 درجة، وفيه طول الضلع ب جـ يساوي 54، وطول الضلع أد يساوي س²+5، فما هي قيمة المتغيرين س، وص؟[٢]
الحل:
- يمكن إيجاد قيمة المتغيرين باستخدام خاصيتين من خصائص متوازي الأضلاع إحداهما أن كل زاويتين متقابلتين متساويتان فالزاوية أ، والزاوية جـ متقابلتان، وبالتالي متساويتان، والأخرى أن كل ضلعين متقابلين متساويان فالضلع ب جـ مقابل للضلع أ د، وبالتالي يساويه.
- إيجاد قيمة س من خلال مساواة طول الضلعين ب جـ، و أد، وذلك كما يلي:
- س²+5=54
- س²=49، وبالتالي فإن س تساوي 7.
- إيجاد قيمة ص من خلال مساواة الزاويتين أ، وجـ، وذلك كما يلي:
- س + 15ص= 127
- 7 + 15ص = 127
- ص = 8.
حساب قيمة س وص لزاويتين في متوازي الأضلاع
متوازي أضلاع د ع هـ و، قاعدته (ع هـ) فيه قياس الزاوية د: 5ص، وقياس الزاوية ع: 115 درجة، وقياس الزاوية هـ: (7س - 5)، فما هي قيمة المتغيرين س، وص؟[٢]
الحل:
- يمكن حل السؤال باستخدام خاصيتين من خصائص متوازي الأضلاع، وهي أن كل زاويتين متحالفتين متكاملتان؛ أي مجموعها 180 درجة، وفي هذا السؤال الزاويتان د، وع متحالفتان، والزاويتان هـ، و متحالفتان، والخاصية الأخرى أن كل زاويتين متقابلتين متساويتان، وفي هذا السؤال الزاوية ع، والزاوية و متقابلتان.
- حساب قيمة ص، وذلك كما يلي:
- 5ص + 115 = 180.
- 5ص = 65.
- ص = 13.
- حساب قيمة س، وذلك كما يلي:
- 115 + (7س - 5) = 180.
- 7س + 110 = 180.
- 7س = 70.
- س = 10.
حساب قيمة ثلاث زوايا مجهولة في متوازي الأضلاع
متوازي أضلاع أ ب جـ د ، وقاعدته (د ج)، فيه قياس الزاوية أ 56 درجة، فما هو قياس زواياه الثلاثة الأخرى؟[٥]
الحل: يمكن إيجاد الزوايا الأخرى باستخدام خصائص متوازي الأضلاع.
- من خصائص متوازي الأضلاع أن كل زاويتين متقابلتين متساويتان، والزاوية أ و جـ هما زاويتان متقابلتان، وبالتالي فهما متساويتان، وبالتالي فإن قياس الزاوية جـ= 56 درجة أيضاً.
- من خصائص متوازي الأضلاع أن كل زاويتين متحالفتين مجموعها 180 درجة، والزاوية د هي زاوية متحالفة مع الزاوية أ، وبالتالي يمكن إيجاد قياسهما كما يلي:
- قياس الزاوية د: 56 + ∠ د = 180
- وبالتالي فإن الزاوية (∠) د قياسها 124 درجة.
- الزاوية ب تقابل الزاوية د، وبالتالي فإن قياسها 124 درجة.
حساب قيمة س وص لأضلاع مجهولة في متوازي الأضلاع
متوازي أضلاع ل م ن هـ، قاعدته (ن هـ) فيه طول الضلع ل م = 6س - 7، وطول الضلع ل ن يساوي ص²+3، وطول الضلع ن هـ يساوي 2س + 9، وطول الضلع م هـ يساوي 12، فما هي قيمة المتغيرين س، وص؟
الحل: يمكن حل هذا السؤال باستخدام إحدى خصائص متوازي الأضلاع، وهي أن كل ضلعين متقابلين متساويان.
- الضلع ل م = الضلع ن هـ، وبالتالي:
- 6س - 7 = 2س + 9
- 4س = 16
- س = 4
- الضلع م هـ = الضلع ل ن، وذلك كما يلي:
- ص²+3=12.
- ص²=9
- ص = 3، أو ص = -3، والطول لا يمكن أن يكون سالباً، وبالتالي فإن قيمة ص تساوي 3.
حساب قيمة س لضلع مجهول في متوازي الأضلاع
متوازي أضلاع أ ن د س، قاعدته (ن د)، وقطراه المستقيمان (أد)، و (س ن) يتقاطعان عند النقطة ع، وفيه طول س ع = 4س - 11، وطول ع ن = س + 10، فما هي قيمة المتغير س؟
الحل: قطرا متوازي الأضلاع ينصفان بعضهما البعض عند النقطة ع، وبالتالي فإن الضلعين س ع و ع ن متساويان، ويمكن إيجاد المتغير س كما يلي:
- 4س - 11 = س + 10
- 3س = 21
- س = 7
المراجع
- ↑ "Parallelogram", www.mathsisfun.com, Retrieved 25-3-2020. Edited.
- ^ أ ب ت ث "Properties of Parallelograms", www.wyzant.com, Retrieved 25-3-2020. Edited.
- ^ أ ب ت "Types of Parallelogram", byjus.com, Retrieved 25-3-2020. Edited.
- ^ أ ب "Sample Problems Involving Quadrilaterals", mathbitsnotebook.com, Retrieved 25-3-2020. Edited.
- ↑ "Properties of Parallelograms", www.ck12.org, Retrieved 25-3-2020. Edited.