محتويات

حساب محيط متوازي المستطيلات
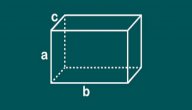
يعد متوازي المستطيلات شكل من الأشكال ثلاثية الأبعاد، ويعتمد حساب محيطه على طوله وعرضه وارتفاعه وبما أنّ فيه 12 ضلعًا، فيُمكن حسابه بالصيغة الرياضية الآتية:[١]
محيط متوازي المستطيلات = 4 × (الطول + العرض + الارتفاع)
وبالرموز:
م = 4 × (س × ص × ع)
حيث أنّ:
- م: محيط متوازي المستطيلات.
- س: طول متوازي المستطيلات.
- ص: عرض متوازي المستطيلات.
- ع: ارتفاع متوازي المستطيلات.
يُعوض في القانون مباشرةً عندما تكون أطوال أبعاده معلومة.
أمثلة على حساب محيط متوازي المستطيلات
وفيما يلي بعض الأمثلة على حساب محيط متوازي المستطيلات:
المثال الأول: جد محيط متوازي المستطيلات الذي يبلغ ارتفاعه 8 سم، وعرضه 10 سم، وطوله 14 سم.
الحل:
- تُكتب المعطيات:
- الارتفاع = 8 سم.
- العرض = 10 سم.
- الطول = 14 سم.
- تُعوض المعطيات في القانون مباشرةً: محيط متوازي المستطيلات = 4 × (الطول + العرض + الارتفاع)
- محيط متوازي المستطيلات = 4 × (14 + 10 + 8)
- محيط متوازي المستطيلات = 128 سم.
المثال الثاني: إذا علمتَ أنّ طول متوازي المستطيلات 18 سم، وعرضه 9 سم، وارتفاعه 7.8 سم، جد محيطه.
الحل:
- تُكتب المعطيات:
- الارتفاع = 7.8 سم.
- العرض = 9 سم.
- الطول = 18 سم.
- تُعوض المعطيات في القانون مباشرةً: محيط متوازي المستطيلات = 4 × (الطول + العرض + الارتفاع)
- محيط متوازي المستطيلات = 4 × (18 + 9 + 7.8)
- محيط متوازي المستطيلات = 139.2 سم.
المثال الثالث: إذا علمتَ أنّ محيط متوازي المستطيلات يساوي 210 سم، وطوله 30 سم، وعرضه 15 سم، فما هو ارتفاعه.
الحل:
- تُكتب المعطيات:
- محيط متوازي المستطيلات = 210 سم.
- العرض = 15 سم.
- الطول = 30 سم.
- تُعوض المعطيات في القانون مباشرةً: محيط متوازي المستطيلات = 4 × (الطول + العرض + الارتفاع)
- 210 = 4 × (30 + 15 + الارتفاع)
- الارتفاع = 7.5 سم.
حساب محيط أحد أوجه متوازي المستطيلات
يتكون متوازي المستطيلات من 6 أوجه مستطيلة الشكل، ويُمكن حساب محيط أحد أوجه متوازي المستطيلات بالخطوات التالية:[٢]
- بما أنّ أوجه متوازي المستطيلات مستطيلة الشكل يُمكن حساب محيطها بقانون محيط المستطيل وهو كالآتي: محيط المستطيل = 2 × (الطول + العرض).[٣]
- ولكن متوازي المستطيلات هو شكل ثلاثي الأبعاد له طول وعرض وارتفاع فإنّ الطول والعرض لكل وجه يختلف عن الآخر ويُمكن حسابهم بأحد القوانين الآتية:
- محيط أحد الأوجه = 2 × (العرض + الارتفاع)
- محيط أحد الأوجه = 2 × (الطول + الارتفاع)
- محيط أحد الأوجه = 2 × (الطول + العرض)
ويُحدد القانون حسب أبعاد الوجه المُراد حساب محيطه.[٢]
أمثلة على حساب محيط أحد أوجه متوازي المستطيلات
فيما يلي بعض الأمثلة على حساب محيط متوازي المستطيلات:
المثال الأول: إذا علمتَ أنّ أبعاد متوازي المستطيلات كالآتي: الطول 8 سم، العرض 6 سم، الارتفاع 4 سم، جد محيط قاعدته.
الحل:
- تُكتب المعطيات:
- الارتفاع = 4 سم.
- العرض = 6 سم.
- الطول = 8 سم.
- أبعاد قاعدة متوازي المستطيلات هي الطول والعرض، وبالتالي سيكون قانون محيط القاعدة كالآتي: محيط قاعدة متوازي المستطيلات = 2 × (الطول + العرض)
- تُعوض المعطيات في القانون:
- محيط قاعدة متوازي المستطيلات = 2 × (الطول + العرض)
- محيط قاعدة متوازي المستطيلات = 2 × (8 + 6)
- محيط قاعدة متوازي المستطيلات = 28 سم.
المثال الثاني: إذا علمتَ أن طول متوازي المستطيلات 22 سم وارتفاعه 7 سم، جد محيط أحد أوجهه الجانبية.
الحل:
- تُكتب المعطيات:
- الارتفاع = 7 سم.
- الطول = 22 سم.
- يُحسب محيط أوجه متوزاي المستطيلات الجانبية باستخدام القانون: محيط أحد الأوجه = 2 × (الطول + الارتفاع)
- تُعوض المعطيات في القانون:
- محيط أحد الأوجه الجانبية = 2 × (22 + 7)
- محيط أحد الأوجه الجانبية = 58 سم.
المثال الثالث: جد طول متوازي المستطيلات الذي يبلغ محيط قاعدته العلوية 68 سم وارتفاعه 12 سم.
الحل:
- تُكتب المعطيات:
- الارتفاع = 12 سم.
- محيط القاعدة = 22 سم.
- تُعوض المعطيات في القانون: محيط قاعدة متوازي المستطيلات = 2 × (الطول + العرض)
- 68 = 2 × (الطول + 12)
- الطول = 22 سم.
يُعرّف متوازي المستطيلات بأنّه شكل ثلاثي الأبعاد يتكون من 6 جوانب غير متساوية في الأبعاد و8 رؤوس و12 ضلعًا، ويُمكن حساب محيطه بجمع جميع أطوال أضلاعه الاثني عشر أو من خلال القانون: محيط متوازي المستطيلات = 4 × (الطول + العرض + الارتفاع)،
كما يُمكن حساب محيط أحد أوجهه باستخدام قانون محيط المستطيل وذلك بناءً على أنّ أوجه متوازي المستطيلات والتي هي أوجه مستطيلة الشكل.'
المراجع
- ↑ "Cube and Cuboid", BYJU'S, Retrieved 23/9/2021. Edited.
- ^ أ ب "Rectangular Prism", BYJU'S, Retrieved 23/9/2021. Edited.
- ↑ "Perimeter of Rectangle", CUEMATH, Retrieved 23/9/2021. Edited.