محتويات

حساب محيط متوازي الأضلاع
يُمكن إيجاد محيط متوازي الأضلاع من خلال استخدام أحد القوانين الآتية:[١]
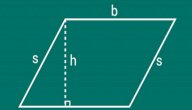
عند معرفة أطوال الأضلاع
فإنّ المحيط هو:
- محيط متوازي الأضلاع= 2×أ + 2×ب = 2×(أ+ب)؛ حيث:
- أ: هو طول أحد ضلعي متوازي الاضلاع المتقابلين، والمتساويين في الطول.
- ب: طول أحد ضلعي متوازي الأضلاع الآخرين المتقابلين، والمتساويين في الطول؛ حيث إن متوازي الاضلاع يحتوي على أربعة أضلاع وكل ضلعين متقابلين فيه متساويان، ومتوازيان.
عند معرفة طول أحد الأضلاع والقطر
فإنّ المحيط هو:
- محيط متوازي الأضلاع=2×أ + الجذر التربيعي للقيمة (2×ق²+2×ل²-4×أ²)، أو محيط متوازي الأضلاع=2×ب+ الجذر التربيعي للقيمة (2×ق²+2×ل²-4×ب²)؛ حيث:
- أ: هو طول أحد ضلعي متوازي الاضلاع المتقابلين، والمتساويين في الطول.
- ب: طول أحد ضلعي متوازي الأضلاع الآخرين المتقابلين، والمتساويين في الطول.
- ق: طول القطر الأول.
- ل: طول القطر الثاني؛ حيث يقسم القطران متوازي الأضلاع إلى مثلثين متطابقين.
عند معرفة طول الضلع والارتفاع وقياس إحدى الزوايا
فإنّ المحيط هو:
- محيط متوازي الأضلاع=2×(ب+ع ب/جاα)، أو محيط متوازي الأضلاع=2×(أ+ع أ/جاα)؛ حيث:
- ع ب: طول العمود الواصل بين الضلع ب والزاوية المقابلة له.
- ع أ: طول العمود الواصل بين الضلع أ والزاوية المقابلة له.
- α: قياس إحدى زوايا متوازي الأضلاع.
أمثلة على حساب محيط متوازي الأضلاع
- المثال الأول: ما محيط متوازي الأضلاع الذي طول أحد أضلاعه 10 وحدات، والضلع الآخر 3 وحدات؟
الحل:
- بما أنّ كلّ ضلعين في متوازي الأضلاع متقابلان ومتساويان، فإنّه يُمكن من خلال معرفة أحد الأضلاع معرفة الضلع الآخر المقابل له، وبالتالي فإنّه يمكن إيجاد محيط متوازي الأضلاع الذي يساوي مجموع أطوال أضلاعه الأربعة، من خلال القانون الآتي:
- محيط متوازي الأضلاع= 2×أ + 2×ب = 2×(أ+ب)
- 2×(3+10)=26 وحدة.
- المثال الثاني: متوازي أضلاع أ ب جـ د طول الضلع أ ب يساوي 12سم، والضلع ب جـ يساوي 7سم، فما هو محيطه؟
الحل:
- محيط متوازي الأضلاع يساوي مجموع اطوال أضلاعه الأربعة، ويُمكن حساب محيطه من خلال القانون الآتي:
- محيط متوازي الأضلاع= 2×أ + 2×ب = 2×(أ+ب)
- 2×(7+12)=38 سم.
- المثال الثالث: متوازي أضلاع (أ ب جـ د) قاعدته (ب ج)، وطول العمود (دو) الساقط من الزاوية د نحو الضلع (ب ج) يساوي 6سم، وطول العمود الواصل بين الزاوية ب والضلع (أد) يساوي 6سم أيضاً، وقياس الزاوية ج يساوي 30 درجة، وطول (ب و) يساوي 20سم، جد محيط متوازي الأضلاع هذا.
الحل:
- يجب أولاً معرفة طول الضلع (أب)، والذي يساوي الضلع (دج)، عن طريق استخدام جيب الزاوية، وهو كالآتي:
- جا(الزاوية ج)=المقابل/الوتر
- (دج)=جا(30)=6/الوتر (دج)، ومنه الوتر (دج)= 12سم، وهو مساوٍ لطول الضلع (أب)، وفق خصائص متوازي الأضلاع.
- حساب طول (وج) عن طريق استخدام نظرية فيثاغورس، لينتج أن:
- طول الوتر(دج)²=طول الضلع الأول (دو)²+طول الضلع الثاني (وج)²
- ومنه: 12²=6²+ (وج)²، ومنه (وج)= 10.39سم.
- حساب طول الضلع (ب ج ) وهو: (ب ج)=(ب و)+(وج)=20+10.39=30.39سم=(أد)، وفق خصائص متوازي الأضلاع.
- محيط متوازي الأضلاع= 2×أ+2×ب = 2×(أ+ب)
- 2×(30.39+12)= 84.78سم.
- المثال الرابع: متوازي أضلاع طول أحد ضلعيه 8 متر، والضلع الآخر 12 متر، وقياس الزاوية بين الضلعين تساوي 60 درجة، فما هو محيطه؟
الحل:
- بما أنّ كل ضلعين متقابلين في متوازي الأضلاع متساويين، ومتوازيين فإنه يمكن إيجاد طولي الضلعين الآخرين، ويساويان 8متر، و12 متر، وبالتالي فإن المحيط وفق قانون محيط متوازي الأضلاع يساوي:
- محيط متوازي الأضلاع= 2×أ+2×ب
- 2×(أ+ب)= 2×(8+12)=40م.م
- المثال الخامس: متوازي أضلاع طول ضلعه يعادل 1/4 طول قاعدته، وطول قاعدته 524مم، فما هو محيطه؟
الحل:
- بما أن طول ضلعه يساوي 1/4 طول القاعدة، فإن طول ضلعه يساوي 524/4، ويساوي 131 مم.
- وبالتالي فإن يمكن حساب محيط متوازي الاضلاع، بمعرفة طول القاعدة، وطول أحد الأضلاع؛ حيث إن كل ضلعين متقابلين في متوازي الأضلاع متساويان، وبالتالي فإن الضلعين الآخرين يساويان 524، و131.
- محيط متوازي الأضلاع= 2×أ+2×ب
- 2×(أ+ب)=2×(131+524)= 1,310مم.
- المثال السادس: متوازي أضلاع (أب ج د) قاعدته (ب ج) طولها 9سم، وارتفاعه (ب و) يساوي 6سم، وطول (أو) يساوي 2سم، جد محيطه.
الحل:
- يمكن إيجاد محيط متوازي الأضلاع باستخدام القاعدة:
- محيط متوازي الأضلاع= 2×(طول القاعدة+طول الضلع الجانبي)
- ولكن طول الضلع الجانبي الذي يمثل الوتر في المثلث القائم المتشكّل بواسطة الارتفاع (ب و) غير موجود، ويمكن إيجاده عن طريق نظرية فيثاغورس.
- (طول الوتر (أب))²=(طول الضلع الأول (أو))²+(طول الضلع الثاني (ب و))²
- ومنه: (طول الوتر (أب))²= 2²+6²=40، ومنه: أب= 40√سم= ج د.
- محيط متوازي الأضلاع= 2×(طول القاعدة+طول الضلع الجانبي)
- 2×(9+40√)سم.
- المثال السابع: متوازي أضلاع (أب ج د) طول قاعدته (ج د) 11 سم، وقياس الزاوية (د) 45 درجة، وارتفاعه يساوي 8 سم، وهو الخط النازل من الزاوية أ إلى الضلع ج د ، أوجد محيطه.
الحل:
- محيط متوازي الأضلاع = 2×(طول الضلع+الارتفاع/جاα)
- 2 × (11 +8 / جا45)
- 2 × (20.41)
- محيط متوازي الأضلاع = 40.80 سم.
- المثال الثامن: متوازي أضلاع طول أحد أضلاعه يساوي 169√سم، فإذا كان طول قاعدته يساوي 5 أضعاف طول ضلعه، فما هو محيطه؟
الحل:
- طول القاعدة يساوي 5 أضعاف طول الضلع، ويساوي 5×169√، ويساوي 5×13=65سم.
- محيط متوازي الأضلاع= 2×(طول القاعدة+طول الضلع)
- 2×(65+13)= 156سم.
- المثال التاسع: متوازي أضلاع (أ ب ج د) فيه: طول القاعدة أب يساوي 5 سم، وطول القطر أج يساوي 7 سم، بينما طول القطر ب د يساوي 6 سم، أوجد محيط متوازي الأضلاع.
الحل:
- محيط متوازي الأضلاع= 2 × طول الضلع + الجذر التربيعي للقيمة (2×(القطر الأول)²+2 ×(القطر الثاني)²- 4× طول الضلع²)
- 2 × 5 + (2×(7)²+2 ×(6)²- 4× 5²)√
- 10 + (70)√
- محيط متوازي الأضلاع= 18.37 سم.
- المثال العاشر: متوازي أضلاع (أب ج د) طول قاعدته (ب ج) 23م، وقياس الزاوية (ب) 45 درجة، وفيه طول الضلع ب و= 5م علماً بأن ارتفاعه هو (أو)، المتمثّل بالعمود النازل من الزاوية أ إلى الضلع (ب ج)، فما هو محيطه؟
الحل:
- حساب الارتفاع باستخدام ظل الزاوية= المقابل/المجاور، ومنه ظا (45)=الارتفاع/5، ومنه الارتفاع=5م.
- محيط متوازي الأضلاع=2×(ب+ع ب /جاα)
- محيط متوازي الأضلاع=2×(5+23/جا45)=60.1سم
- المثال الحادي عشر: إذا علمتَ أنّ محيط متوازي الأضلاع يساوي 20 سم، وطول قاعدته يساوي 4 سم، أوجد طول الضلع الجانبي للمتوازي.
الحل:
- تطبيق قانون محيط متوازي الأضلاع:
- محيط متوازي الأضلاع = 2 × (طول القاعدة + طول الضلع الجانبي)
- 20 = 2 × (4 + طول الضلع الجانبي)
- 10 = 4 + طول الضلع الجانبي
- طول الضلع الجانبي = 6 سم.
- المثال الثاني عشر: إذا علمتَ أنّ محيط متوازي الأضلاع يساوي 50 سم، وطول ضلع الجانبي يساوي 7 سم، أوجد طول قاعدة متوازي الأضلاع.
الحل:
- تطبيق قانون محيط متوازي الأضلاع:
- محيط متوازي الأضلاع = 2 × (طول القاعدة + طول الضلع الجانبي)
- 50 = 2 × (طول القاعدة + 7)
- 25 = طول القاعدة + 7
- طول القاعدة = 18 سم.
- المثال الثالث عشر: احسب محيط متوازي الأضلاع الذي يبلغ طول قاعدته 3 سم وطول ضلعه الجانبي 6 سم.
الحل:
- تطبيق قانون محيط متوازي الأضلاع:
- محيط متوازي الأضلاع = 2 × (طول القاعدة + طول الضلع الجانبي)
- 2 × (3 + 6)
- محيط متوازي الأضلاع = 18 سم.
نظرة عامة حول محيط متوازي الأضلاع
يُعرف المحيط باللغة الإنجليزية بالمصطلح (Perimeter) المشتق من الكلمة اليوناينة (peri) التي تعني حول، والكلمة (meter) وهي وحدة قياس المسافة، وبالتالي فإن المحيط هو المسافة المحيطة بالشكل ثنائي الأبعاد،[٢] ومحيط متوازي الأضلاع هو مجموع أطوال أضلاعه الأربعة كغيره من الأشكال الرباعية ثنائية الأبعاد.[٣]
المحيط هو الحدود الخارجية للشكل ثنائي الأبعاد، ويُمكن حساب محيط متوازي الأضلاع بجمع جميع أطوال أضلاعه الأربعة أو باستخدام القانون: 2 × (طول الضلع الأول (طول القاعدة) + طول الضلع الثاني (الطول الجانبي))، كما يُمكن حساب محيط متوازي الأضلاع إذا علمنا طول أحد أضلاعه وقطره، أو بمعرفة طول أحد أضلاعه وارتفاعه وقياس إحدى زواياه.
المراجع
- ↑ "Parallelogram. Formulas and Properties of a Parallelogram", onlinemschool.com, Retrieved 20-3-2020. Edited.
- ↑ "How to find the perimeter of a parallelogram", www.moomoomath.com, Retrieved 20-3-2020. Edited.
- ↑ "Perimeter of a Parallelogram", byjus.com, Retrieved 20-3-2020. Edited.