محتويات

حساب أبعاد المستطيل عند معرفة المساحة
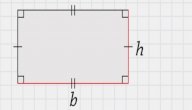
تتكون الأشكال الهندسيّة من أبعاد تكونها وهي الطول والعرض والارتفاع، وأحيانًا تكون الأبعاد متساوية أو غير متساوية وفقًا لخصائص الشكل الهندسي، ومن خلال هذه الأبعاد نستطيع حساب المساحة والمحيط والحجم، أما فيما يتعلق بأبعاد المستطيل فهي الطول والعرض، ولحساب قيمة أبعاد المستطيل، يجب معرفة مساحة المستطيل، وأحد الأبعاد، فمثلًا؛ لحساب عرض المستطيل يجب معرفة مساحته وطوله، والعكس صحيح في حالة حساب طول المستطيل، ولكل من الحالتين قانونًا لإيجاد قيمتها، مشتق من القانون الرئيسي لحساب مساحة المستطيل وهو؛ مساحة المستطيل = الطول × العرض، وبالرموز؛ م= أ × ب،[١][٢] وفيما يأتي كيفية إيجاد أبعاد المستطيل اعتمادًا على قانون مساحته:
قانون طول المستطيل عند معرفة المساحة
يُحسب عرض المستطيل بالقانون التالي:[١][٢]
عرض المستطيل = مساحة المستطيل/ طول المستطيل
وبالرموز؛ ب = م / أ، حيث أن:
- ب: عرض المستطيل
- م: مساحة المستطيل.
- أ: طول المستطيل.
وفيما يلي مثال يوضّح كيفية إيجاد عرض المستطيل:
مثال
احسب عرض مستطيل مساحته 40 م²، وطوله 10 م.
- الحل:
- تعوّض القيم في المعادلة: ب = م/ أ.
- ب= 40 / 10
- إذًا فعرض المستطيل = 4 م.
قانون عرض المستطيل عند معرفة المساحة
يُحسب طول المستطيل من خلال العلاقة التالية:[٢]
طول المستطيل= مساحة المستطيل/ عرض المستطيل
وبالرموز؛ أ = م / ب، حيث أن:
- أ: طول المستطيل.
- ب: عرض المستطيل
- م: مساحة المستطيل.
مثال
احسب طول مستطيل مساحته 20 م²، وعرضه 3 م.
- الحل:
- تعوض القيم في القانون: أ = م / ب
- ومنه؛ أ = 20 / 3
- إذًا (أ= عرض المستطيل= 6.67 م).
يمكن حساب أبعاد المستطيل عند معرفة مساحته من خلال القوانين المشتقة من قانون مساحة المستطيل، فلحساب طول المستطيل يستخدم القانون؛ طول المستطيل= مساحة المستطيل/ عرض المستطيل، ولحساب عرضه يستخدم القانون؛ عرض المستطيل = مساحة المستطيل/ طول المستطيل.
حساب أبعاد المستطيل عند معرفة المُحيط
يعرف محيط المستطيل بأنه مجموع أطوال أضلاعه الأربعة، وهو مجموع الطولين ومجموع العرضين، ولمعرفة أبعاد المستطيل عند معرفة المحيط يجب معرفة أحد الأبعاد؛ فلحساب عرضه يحب معرفة محيطه وطوله، ولحساب طوله يجب معرفة محيطه وعرضه، ولكل حالة قانون للحساب مشتق من قانون محيط المستطيل، والذي يكون على الصيغة الرياضية الآتية: محيط المستطيل= مجموع أطوال أضلاعه= (2 × الطول) + (2 × العرض)، وبالرموز م = (2 × أ) + (2 × ب)،[٣] وفيما يأتي طريقة إيجاد أبعاد المستطيل عند معرفة محيطه:
قانون طول المستطيل عند معرفة المُحيط
لحساب قيمة طول المستطيل يجب معرفة قيمة عرضه ومحيطه، باستخدام القانون التالي:[٣]
طول المستطيل= ((محيط المستطيل - (2 × عرض المستطيل)) / 2
وبالرموز؛ أ = ((م - ( 2 × ب))/ 2، حيث أن:
- ب: عرض المستطيل.
- م: مساحة المستطيل.
- أ: طول المستطيل.
مثال
احسب طول مستطيل، محيطه 28 م، وعرضه 6 م.[٤]
- الحل:
- باستخدام القانون؛ أ= ((م- (2 × ب))/ 2.
- نعوض القيم في القانون: أ = ((28 - (2×6))/2.
- أ = ((28- ( 12))/2.
- أ = 16/ 2.
- أ = طول المستطيل = 8 م.
قانون عرض المستطيل عند معرفة المُحيط
لحساب قيمة عرض المستطيل يجب معرفة قيمة طول ومحيط المستطيل، باستخدام القانون التالي:[٥]
عرض المستطيل= ((محيط المستطيل - (2× طول المستطيل))/ 2
وبالرموز ب =(( م - (2 × أ))/ 2، حيث أن:
- ب: عرض المستطيل
- م: مساحة المستطيل.
- أ: طول المستطيل.
مثال
احسب عرض مستطيل محيطه 22 م، وطوله 8 م.[٦]
- الحل:
- باستخدام القانون: ب= ((م - (2 × أ)) / 2
- نعوض في القانون: ب = ((22 - (2 × 8))/ 2
- ب = ((22 - (16))/ 2
- ب = 6/ 2
- ب = عرض المستطيل = 3 م
يمكن حساب أبعاد المستطيل عند معرفة محيطه من خلال القوانين المشتقة من قانون محيط المستطيل، فلحساب طول المستطيل يستخدم القانون؛ طول المستطيل= ((محيط المستطيل - (2 × عرض المستطيل)) / 2، ولحساب عرضه يستخدم القانون؛ عرض المستطيل= ((محيط المستطيل - (2× طول المستطيل))/ 2 .
حساب أبعاد المستطيل عند معرفة القُطر وأحد الأبعاد
للمستطيل قطران متقاطعان يقسمان المستطيل لمثلثاث، ويُحسب قطر المستطيل، بالمعادلة التالية: طول قطر المستطيل= الجذر التربيعي للقيمة (الطول² + العرض²)، وبالرموز ق = (أ² + ب²)√،[٥] ويمكن إيجاد أبعاد المستطيل عند معرفة قطره وأحد أبعاده باتباع الخطوات التالية:
قانون طول المستطيل عند معرفة القُطر وأحد الأبعاد
يُحسب طول المستطيل عند معرفة قيمة القطر والعرض، بقانون القطر السابق ق = (أ² + ب²)√ وبالتعويض في القيم المعطاة نحصل على قيمة طول المستطيل، أو بالقانون المشتق منه:[٧]
الطول²= القطر² × العرض²
وبالرموز؛ أ² = ق²- ب²، حيث أن:
- أ: طول المستطيل.
- ق: قطر المستطيل.
- ب: عرض المستطيل.
مثال
احسب طول المستطيل الذي طول قطره يساوي 5 م، وعرضه 4 م.[٥][٧]
- الحل (1):
- باستخدام القانون: ق = (أ² + ب²)√
- تُعوّض قيم القطر والعرض في المعادلة: 5 = (أ² + 4²)√
- يُربع جانبي المعادلة فيذهب الجذر التربيعي: 25 = (أ² + 16)
- يُنقل العدد 16 لجانب المعادلة الآخر وذلك بطرح من نفسه: 25- 16 = أ²
- أ² = 9
- يُؤخذ الجذر التربيعي للطرفان، لينتج أنّ طول المستطيل= 3 م.
- الحل (2):
- باستخدام قانون: أ² = ق² - ب²
- تُعوّض القيم: أ² = 25 - 16
- أ² = 9
- يؤخذ الجذر التربيعي للطرفان
- طول المستطيل= 3 م.
قانون عرض المستطيل عند معرفة القُطر وأحد الأبعاد
يُشتق قانون عرض المستطيل من قانون حساب القطر، وهو:[٧]
العرض² = القطر² - الطول²
وبالرموز؛ ب² = ق² - أ²، حيث أن:
- أ: طول المستطيل.
- ق: قطر المستطيل.
- ب: عرض المستطيل.
مثال
احسب عرض مستطيل الذي طول قطره 5 سم، وطول ضلعه 4 سم.[٥][٧]
- الحل:
- باستخدام القانون: ب² = ق² - أ²
- تعوض القيم؛ ب²= 5 ²- 4 ²
- ب² = 25 - 16
- ب² = 9
- يُؤخذ الجذر التربيعي: ب² √ = 9 √
- العرض (ب) = 3 سم.
- يمكن استخدام القانون ق = (أ² + ب²)√ لحساب عرض المستطيل بتعويض قيم الطول والقطر فقط.
يمكن حساب أبعاد المستطيل عند معرفة قطره وأحد الأبعاد من خلال القوانين التالية، فلحساب طول المستطيل يستخدم القانون؛ الطول²= القطر² × العرض²، ولحساب عرضه يستخدم القانون؛ العرض² = القطر² - الطول².
حساب أبعاد المستطيل عند معرفة القُطر والزاوية المحصورة
يمكن حساب طول وعرض المستطيل عند معرفة قطره والزاوية المحصورة بين القطر وأحد البعدين من خلال تطبيق القوانين:
قانون طول المستطيل عند معرفة القُطر والزاوية المحصورة
يُحسب طول المستطيل عند معرفة قيمة القطر والزاوية المحصورة بينه وبين الطول بالقانون التالي:[٧]
قطر المستطيل = الطول/ جتا (الزاوية/ 2)
وبالرموز ق = أ × جتا (α /2)، حيث أن:
- ق: قطر المستطيل.
- أ: طول المستطيل.
- α: الزاوية المحصورة بين القطر والطول.
مثال
احسب طول المستطيل، الذي قطره 5 سم، والزاوية المحصورة بينهما تساوي 60 درجة.
- الحل:
- باستخدام؛ القانون ق = أ/ جتا (α /2)
- نعوض القيم: 5 = أ/ جتا(60/2)
- 5 = أ/ جتا (30)
- 5 = أ/0.15
- ننقل المتغيرات: 5 ×0.15 = أ
- أ = الطول = 0.75 سم.
قانون عرض المستطيل عند معرفة القُطر والزاوية المحصورة
يُحسب عرض المستطيل، عند معرفة قيمة القطر والزاوية المحصورة بينه وبين العرض بالقانون التالي:[٧]
قطر المستطيل = العرض/ جيب (الزاوية / 2)
وبالرموز ق = ب/ جا (α /2)، حيث أن:
- ق: قطر المستطيل.
- ب: عرض المستطيل.
- α: الزاوية المحصورة بين القطر والعرض.
مثال
احسب عرض المستطيل، الذي قطره يساوي 5 سم، والزاوية المحصورة بينهما تساوي 60 درجة.
- الحل:
- باستخدام القانون؛ ق = ب/ جا (α /2)
- نعوض القيم: 5 = ب/ جا (60/2)
- 5 = ب/ جا (30)
- 5 = ب/ 0.5
- ننقل المتغيرات: 5× 0.5 = أ
- ب = العرض = 2.5 سم
يمكن حساب أبعاد المستطيل عند معرفة قطره والزاوية المحصورة بين القطر وأحد الأبعاد من خلال القوانين التالية، فلحساب طول المستطيل يستخدم القانون؛ قطر المستطيل = الطول/ جتا (الزاوية/ 2)، ولحساب عرضه يستخدم القانون؛ قطر المستطيل = العرض/ جيب (الزاوية / 2).
المراجع
- ^ أ ب "Dimensions - Definition with Examples", Splash Learn, Retrieved 16/6/2021. Edited.
- ^ أ ب ت By Chris Deziel (3/11/2020), "How to Find the Length and Width of a Rectangle When Given the Area", SCIENCING, Retrieved 16/6/2021. Edited.
- ^ أ ب "Perimeter of Rectangle", cuemath, Retrieved 16/6/2021. Edited.
- ↑ "Basic Geometry : How to find the length of the side of a rectangle", varsitytutors, Retrieved 9/8/2021. Edited.
- ^ أ ب ت ث "How to Find the Width of a Rectangle", wikihow, 22/1/2021, Retrieved 16/6/2021. Edited.
- ↑ "Basic Geometry : How to find the length of the side of a rectangle", varsitytutors, Retrieved 9/8/2021. Edited.
- ^ أ ب ت ث ج ح By Dominik Czernia, PhD candidate (30/10/2020), "Diagonal of a Rectangle Calculator", omni CALCULATER, Retrieved 16/6/2021. Edited.