محتويات

طرق حساب ارتفاع المثلث
يُعرّف ارتفاع المثلث (بالإنجليزية: Triangle Altitude) بأنّه الخط المُمتدّ من أحد رؤوس المثلث (وهو النقطة التي يلتقي عندها ضلعان من أضلاع المثلث الثلاث)، وحتى الضلع المقابل له، ويكون عمودياً عليه،[١] وبالتالي فإن للمثلث ثلاثة ارتفاعات ممكنة، ويعتبر الارتفاع أقصر مسافة تصل بين رأس المثلث والضلع المقابل له،[٢] وهناك العديد من الطرق لحساب ارتفاع مثلث ما، ومنها:
باستخدام قانون مساحة المثلث
يتم حساب ارتفاع المثلث إذا عُلمت مساحته وطول قاعدته بواسطة قانون مساحة المثلث، وذلك لجميع أنواع المثلثات، وذلك كما يلي:[٣]
- قانون مساحة المثلث = 1/2× القاعدة × الارتفاع، ويمكن إعادة ترتيبه لحساب ارتفاع المثلث كالآتي:
- الارتفاع = (2×المساحة) / القاعدة
- وبالرموز:
- ع = (2×م) / ق
- حيث:
- ع: ارتفاع المثلث.
- م: مساحة المثلث.
- ق: طول قاعدة المثلث.
فمثلاً إذا كان هناك مثلث مساحته 20 سم2 وطول قاعدته 4 سم، فإن ارتفاعه هو:[٤]
- بتعويض القيم المعطاة في قانون المساحة ينتج أنّ:
- الارتفاع = (2×المساحة)/القاعدة
- (2×20) / 4 =10 سم.
باستخدام نظرية فيثاغورس
يمكن حساب ارتفاع المثلث قائم الزاوية أو المثلث متساوي الساقين باستخدام نظرية فيثاغورس وذلك كما يأتي:
المثلث قائم الزاوية
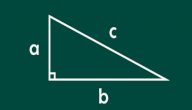
يمكن حساب ارتفاع المثلث قائم الزاوية باستخدام نظرية فيثاغورس إذا عُلم طول قاعدته ووتره وفقا للصيغة الآتية:[٥]
- الوتر² = القاعدة² + الارتفاع²، وبترتيب المعادلة تصبح:
الارتفاع = (الوتر² - القاعدة²)√.
- فمثلاً إذا كان هناك مثلث قائم الزاوية طول قاعدته 6 سم، وطول الوتر فيه 7 سم، فإن ارتفاعه هو:[٥]
- بتعويض القيم المعطاة في نظرية فيثاغورس ينتج أن:
- الارتفاع = (الوتر² - القاعدة²)√ = (7² - 6²)√
- (49 - 36)√ = 13√، ويساوي تقريبا 3.6 سم.
المثلث متساوي الساقين
يُمكن استخدام نظرية فيثاغورس في معرفة ارتفاع المثلث متساوي الساقين إذا عُلم طول قاعدته وطول أحد ضلعيه المتساويين، وذلك باتباع الخطوات الآتية:[٦]
- تقسيم المثلث متساوي الساقين عن طريق إسقاط عمود من الرأس على القاعدة، فيتكون مثلثان قائما الزاوية ومتطابقان، ويشكل العمود الساقط الضلع الأول أو الارتفاع للمثلث قائم الزاوية وللمثلث متساوي الساقين.
- اعتبار طول أحد الضلعين المتساويين هو طول الوتر.
- اعتبار طول نصف قاعدة المثلث متساوي الساقين هو الضلع الثاني أو قاعدة المثلث قائم الزاوية.
- تطبيق قانون نظرية فيثاغورس: الوتر² = القاعدة² + الارتفاع²، وبترتيب المعادلة تصبح: الارتفاع = (الوتر² - القاعدة²)√.
- فمثلاً إذا كان هناك مثلث متساوي الساقين طول أحد ضلعيه المتساويين 5 سم، وطول قاعدته 6 سم، فما ارتفاعه؟[٧] بتطبيق الخطوات السابقة:
- تقسيم المثلث متساوي الساقين بإسقاط عمود من الرأس إلى القاعدة، فيتكون مثلثان قائما الزاوية ومتطابقان.
- تطبيق نظرية فيثاغورس على أحد المثلثين قائمي الزاوية واعتبار أن طول الوتر = 5 سم، وطول قاعدة مثلث قائم الزاوية = 3 سم.
- تطبيق قانون نظرية فيثاغورس: الارتفاع = (الوتر² - القاعدة²)√ = (5² - 3²)√ = 4 سم.
باستخدام الاقترانات المثلثية
يمكن استخدام الاقترانات المثلثية لحساب ارتفاع المثلث القائم أب ج، أو المثلث متساوي الساقين بعد إسقاط عمود من رأسه نحو قاعدته، وذلك عند معرفة قياس إحدى زواياه، وأحد أضلاعه، وذلك كما يلي:
- جيب الزاوية= الضلع المقابل للزاوية/الوتر.
- جيب تمام الزاوية= الضلع المجاور للزاوية/الوتر.
- فمثلاً إذا كان هناك مثلث متساوي الساقين طول ساقيه 10 سم، وقياس الزاوية المحصورة بينهما 120°، فإن ارتفاعه هو:[٨]
- بتطبيق الخطوات الآتية:
-
- إسقاط عمود من رأس المثلث بحيث ينصّف زاوية الرأس إلى منتصف قاعدته، ليتكون مثلثان قائما الزاوية ومتطابقان، ليتمثّل الوتر بإحدى ساقي المثلث متساوي الساقين، أما زاوية الرأس فقياسها 120/2= 60°.
- باستخدام قانون جتا س = الضلع المُجاور للزاوية س/ الوتر، وباعتبار أن الارتفاع هو الضلع المجاور للزاوية ينتج أن:
- جتا س = الارتفاع / الوتر، ومنه: جتا 60° = الارتفاع / 10
- وبضرب طرفي المعادلة بالعدد 10 ينتج أن: الارتفاع = جتا 60°×10= 5 سم.
طريقة حساب ارتفاع المثلث متساوي الأضلاع
المثلث المتساوي الأضلاع هو مثلث تتساوى فيه جميع أضلاعه وجميع زواياه وتساوي 60 درجة، وتتساوي فيه أيضاً قيمة ارتفاعاته الثلاث، التي يمكن حسابها مباشرة من خلال العلاقة الرياضية الآتية:[٣]
- الارتفاع = (طول الضلع×3√) / 2
- فمثلاً إذا كان هناك مثلث متساوي الأضلاع طول ضلعه 12 سم فإن ارتفاعه هو:[٩]بتعويض القيم المعطاة في العلاقة السابقة ينتج أن:
- الارتفاع = (طول الضلع×3√) / 2 = (12×3√) / 2= 3√6 = 10.39 سم تقريباً
يمكن أيضاً حساب ارتفاع المثلث متساوي الأضلاع باستخدام نظرية فيثاغورس وذلك بتطبيق نفس الخطوات السابقة المتّبعة في حساب ارتفاع المثلث متساوي الساقين.[٤]
طرق أخرى لحساب ارتفاع المثلث
يمكن حساب ارتفاع المثلث مهما كان نوعه بطرق أخرى تتمثّل بما يلي:[٤]
- عند معرفة طول ضلعين والزاوية المحصورة بينهما، يمكن حساب مساحة المثلث بالصيغة الآتية:
- مساحة المثلث = ½ × الضلع الأول (القاعدة) × الضلع الثاني المجاور للقاعدة × جا (الزاوية المحصورة بينهما)
- ثم تعويض قيمة المساحة وطول القاعدة في القانون: الارتفاع = (2×المساحة)/القاعدة، للحصول على قيمة الارتفاع.
- عند معرفة أطوال الأضلاع الثلاثة للمثلث: يمكن حساب مساحة المثلث باستخدام صيغة هيرون، وهي:
- المساحة= (س(س-أ)(س-ب) (س-ج))√
- حيث:
- س: نصف محيط المثلث= (أ+ب+ج)/2.
- أ، ب، ج: أطوال أضلاع المثلث الثلاثة.
ثم تعويض قيمة المساحة وطول القاعدة في القانون: الارتفاع = (2×المساحة)/القاعدة، للحصول على قيمة الارتفاع.
أمثلة متنوعة على حساب ارتفاع المثلث
- المثال الأول: إذا كان هناك مثلث متساوي الساقين طول أحد ضلعيه المتساويين 13 سم، وطول قاعدته 10 سم، فما ارتفاعه؟[١٠]
الحل:
- تقسيم المثلث متساوي الساقين بإسقاط عمود من الرأس إلى القاعدة، فيتكون مثلثان قائما الزاوية ومتطابقان.
- تطبيق نظرية فيثاغورس على أحد المثلثين قائمي الزاوية واعتبار أن طول الوتر = 13سم، وطول قاعدة مثلث قائم الزاوية = 5 سم.
- تطبيق قانون نظرية فيثاغورس: الارتفاع = (الوتر² - القاعدة²)√ = (13² - 5²)√ = 12 سم.
- المثال الثاني: إذا كانت مساحة مثلث قائم الزاوية 28سم²، وطول قاعدته 7سم، جد ارتفاعه.[١١]
الحل:
- بتطبيق قانون: الارتفاع = (2×المساحة)/القاعدة = (2×28)/7 = 8سم.
- المثال الثالث: إذا كان طول قاعدة مثلث قائم الزاوية 3سم، وطول وتره 5سم، جد ارتفاعه.[١١]
الحل:
- تطبيق قانون نظرية فيثاغورس: الارتفاع = (الوتر² - القاعدة²)√ = (5² - 3²)√ = 4 سم
- المثال الرابع: إذا كانت أطوال أضلاع احد المثلثات: 13، 14، 15 سم، جد ارتفاعه.[١٢]
الحل:
- بتطبيق صيغة هيرون: المساحة= (س(س-أ)(س-ب) (س-ج))√،
- وحساب قيمة س: (أ+ب+ج)/2 = (13+14+15) /2 = 21،
- ومنه المساحة= (21(21-13)(21-14) (21-15))√ = 84 سم².
- بتطبيق قانون: الارتفاع = (2×المساحة)/القاعدة، واختيار 14سم لتمثل قاعدة المثلث
- ينتج أن: الارتفاع= (2×84)/ 14 = 12 سم.
- المثال الخامس: إذا كان طول ضلع المثلث متساوي الأضلاع يساوي 10سم، جد ارتفاعه.[١٣]
الحل:
- بتطبيق قانون: الارتفاع = (طول الضلع × 3√) / 2 = (10×3√)/2 = 3√5 سم
- المثال السادس: إذا كان طول محيط مثلث متساوي الأضلاع يساوي 18سم، جد ارتفاعه.[١٤]
الحل:
- لحساب الارتفاع يجب أولاً حساب طول ضلع المثلث متساوي الأضلاع من القانون:
- محيط المثلث متساوي الأضلاع= 3×طول الضلع، ومنه: طول الضلع = 18/3= 6سم.
- تطبيق قانون: الارتفاع = (طول الضلع×3√) / 2 = (6×3√)/2 = 3√3 سم.
- المثال السابع: إذا كانت مساحة مثلث مختلف الأضلاع 17.7، وطول قاعدته هو 4سم، جد ارتفاعه.[١٤]
الحل:
- بتطبيق قانون: الارتفاع = (2×المساحة)/القاعدة = (2×17.7)/4 = 8.85سم.
- المثال الثامن: إذا كان طول الضلع ب ق في المثلث (ب ق ر) هو 4.3سم، والضلع ق ر= 6.5سم، والزاوية (ب ق ر)= 39 درجة، فما هو ارتفاعه على افتراض أن قاعدته هي (ب ق).[١٥]
الحل:
- باستخدام القانون:
- مساحة المثلث = ½ × الضلع الأول (القاعدة) × الضلع الثاني المجاور للقاعدة × جا (الزاوية المحصورة بينهما)
- ينتج أن: مساحة المثلث= ½ × 4.3 × 6.5 × جا (39) = 8.81 سم².
- تعويض القيم في القانون: الارتفاع = (2×المساحة)/القاعدة (2×8.81)/4.3 = 4.1سم، وهو العمود النازل من الرأس ر نحو القاعدة (ب ق).
المراجع
- ↑ "Triangle Altitude Theorem", Easy Calculation, Retrieved 10-11-2017. Edited.
- ↑ "Altitude of a triangle", www.mathopenref.com, Retrieved 14-4-2019. Edited.
- ^ أ ب Hanna Pamuła, "Triangle Height Calculator"، www.omnicalculator.com, Retrieved 18-4-2019. Edited.
- ^ أ ب ت "How to Find the Height of a Triangle", www.wikihow.com, Retrieved 18-4-2019. Edited.
- ^ أ ب "The Pythagorean Theorem", www.montereyinstitute.org, Retrieved 11-4-2019. Edited.
- ↑ "How to Find the Height of a Triangle", www.wikihow.com,updated 29-3-2019، Retrieved 14-4-2019. Edited.
- ↑ "How to Find the Area of an Isosceles Triangle", www.wikihow.com, Retrieved 18-4-2019. Edited.
- ↑ "How to Find the Area of an Isosceles Triangle", www.wikihow.com, Retrieved 14-42019. Edited.
- ↑ "Area of an Equilateral Triangle", www.mathcaptain.com, Retrieved 18-4-20019. Edited.
- ↑ "The side of a triangle is 16 inches.", mathcentral.uregina.ca, Retrieved 9-4-2020. Edited.
- ^ أ ب " How to find the height of a right triangle Example Question #1 : How To Find The Height Of A Right Triangle", www.varsitytutors.com, Retrieved 9-4-2020. Edited.
- ↑ "height of a triangle", mathcentral.uregina.ca , Retrieved 9-4-2020. Edited.
- ↑ "Lesson 1 Rules for triangles", www.rasmus.is, Retrieved 9-4-2020. Edited.
- ^ أ ب "Find the Height of a Triangle", www.mathwarehouse.com, Retrieved 12-4-2020. Edited.
- ↑ "Area of Triangles", www.onlinemathlearning.com, Retrieved 12-4-2020. Edited.