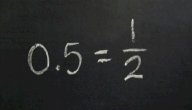محتويات

مفهوم النسبة المئوية
يُمكن تعريف النسبة المئوية (بالإنجليزية: Percent) بأنها النسبة التي يشكّل العدد مئة الجزء الثاني منها، وتعود كلمة النسبة المئوية في أصلها إلى الكلمة اللاتينية (Per Centum)، والتي تَعني لكل مئة، وعادة يُعبّر عنها رياضياً بالرمز (%)،[١] ويمكن التعبير عنها كذلك بأشكال أخرى بعد تحويلها إلى كسور عادية أو عشرية؛ فعلى سبيل المثال يمكن كتابة النصف على شكل النسبة المئوية (50%)، أو العدد العشري (0.5)، أو الكسر العادي (1/2)،[٢] ومن الأمثلة الأخرى على النسب المئوية: 100%=100/100=1، 40%=40/100=4/10=2/5=0.4.[٣]
يمكن توضيح مفهوم النسبة المئوية بشكل أكثر بساطة من خلال تخيّل تقسيم بيتزا كبيرة مثلاً إلى مئة جزء صغير، ففي هذه الحالة يشكّل كل جزء من هذه الأجزاء نسبة 1% من البيتزا، أما ربع البيتزا فهو يشكل نسبة 25% منها، أما البيتزا كاملة فيعبّر عنها بنسبة 100%،[٤] ومن الأمثلة الواقعية كذلك هو التعبير عن عدد الأيام الماطرة من مجموع الأيام الكلي خلال فترة معيّنة من الفترات على شكل نسبة مئوية؛ فمثلاً إذا كان الجو ماطراً لمدة امتدت لأربعة عشر يوماً خلال مدة مئة يوم فائتة، فإنه يمكن التعبير عن ذلك كنسبة مئوية على شكل 14/100=14%، وهذا يعني أن 14 يوماً كان ماطراً من أصل 100 يوم خلال الفترة السابقة،[٥] كما أن قول إن محتويات هذه الصندوق مكوّنة بنسبة 75% من التفاح فهذا يعني أن التفاح يكوّن 75 غرضاً من كل 100 غرضٍ من محتوياته.[٦]
حساب النسبة المئوية
تُعرّف النسبة المئوية بأنها عملية إسناد أي رقم إلى مئة، ويُمكن تحويل أي رقم إلى نسبة مئوية من خلال اتباع ما يلي حسب حالته:[٧]
- حساب النسبة المئوية لنظام معين: تعتبر النسبة المئوية طريقة يمكن من خلالها التعبير عن أحد الأعداد كجزء أو حصة من مجموعة من الأعداد،[٧] ويمكن حسابها باستخدام الصيغة العامة أو القانون الآتي: النسبة المئوية= (القيمة/القيمة الكلية)×100%،[٨] أو النسبة المئوية= (الجزء/الكل)× 100%،[٦] وعليه يُمكن حساب النسبة المئوية لنظام ما من خلال تَقسيم عدد الأفراد أو الحاجيات المُراد معرفة نسبتها على العدد الكُلي للمجتمع أو الحاجيات المَشمولة في هذه الدراسة، وضرب الناتج النهائي بالعدد 100؛ فمثلاً يمكن حساب نسبة الأفراد المالكين لبطاقة اشتراك مكتبية إذا كان عددهم 38 فرداً ضمن مجتمع معين يبلغ عدده 230 فرداً، عن طريق تعويض الأعداد في المعادلة السابقة، لينتج أن 38/230× 100%=16.5%، وذلك يعني أن 16.5 فرداً من كل 100 فرد من الأفراد في ذلك المجتمع يمتلكون بطاقة مكتبية، او أن نسبة 16.5% من ذلك المجتمع يمتلكون بطاقة مكتبية.[٧]
- تحويل الكسر العادي إلى نسبة مئوية: يتكوَّن أي كسر عادي من بسط ومقام، حيث يتمثل البسط بالعدد الموجود في الأعلى، أما المقام فهو العدد الموجود في الأسفل، وعند تحويل الكسر إلى نسبة مئوية فإن ذلك يعني جعل المقام مساوياً للعدد 100، ويتطلب تحقيق ذلك ضرب العدد الموجود في المقام برقم آخر مناسب لجعله مساوياً للعدد 100، وضرب البسط كذلك بنفس هذا العدد؛ وذلك للحفاظ على قيمة الكسر دون تغيير، فعلى سبيل المثال يمكن تحويل الكسر 4/25 إلى نسبة مئوية عن طريق ضرب كل من البسط والمقال بالعدد 4، لينتج أن 4/25=16/100=16%، وفي المقابل يمكن تحويل النسبة المئوية ببساطة إلى كسر عادي عن طريق وضع قيمة النسبة المئوية على مقام قيمته العدد 100، ثم تبسيط الكسر إلى أبسط صورة ممكنة، فمثلاً يتطلب تحويل النسبة 50% إلى كسر عادي، كتابة العدد 50% على هيئة 50/100، ثم تبسيط الكسر كما يأتي: 50/100=5/10=1/2.[٩][٧]
- تحويل العدد العشري إلى نسبة مئوية: تعتبر هذه العملية الأبسط مقارنة بما سبق، حيث يتطلب تحويل العدد العشري إلى نسبة مئوية ضرب هذا العدد فقط بالعدد مئة وإضافة علامة % إلى الناتج، فعلى سبيل المثال يمكن تحويل العدد 0.8 إلى نسبة مئوية عن طريق ضربة العدد 100 لينتج أن 0.8×100=80%، 1.34×100=134%، وفي المقابل يمكن تحويل النسبة المئوية إلى عدد عشري عن طريق عكس العملية السابقة وذلك بقسمة النسبة المئوية على العدد 100، فلتحويل النسبة 56% إلى عدد عشري يمكن القيام بذلك ببساطة عن طريق قسمة 56 على 100 لينتج أن 56/100=0.56=56%.
لمزيد من المعلومات حول النسبة والتناسب يمكنك قراءة المقال الآتي: شرح النسبة والتناسب.
العمليات الحسابية على النسب المئوية
من أبسط العمليات الحسابية على النسب المئوية ما يأتي:[١٠][١١]
- جمع وطرح النسب المئوية: يتطلب جمع أو طرح النسب المئوية تحويلها أولاً إلى أعداد عشرية، أو كسور عادية؛ فمثلاً يتطلب جمع نسبة 37% و نسبة 42% تحويلهما إلى أعداد عشرية أولاً، ثم جمع هذه الأعداد كما يأتي: 0.37+0.24=0.79=79%.
- ضرب وقسمة النسب المئوية: يتطلب ضرب النسب المئوية أو قسمتها كتابتها أولاً على شكل أعداد عشرية أو كسور عادية، فمثلاً يتطلب ضرب النسب الآتية: 10%، 20%، 30% ببعضها تحويلها أولاً إلى كسور عادية، ثم ضربها كالمعتاد، كما يأتي: 10/100×20/100×30/100=6/1000=0.6%
تطبيقات عملية على النسبة المئوية
يُمكن استخدام النسبة المئوية في العديد المجالات مثل حساب مقدار الخصم على سلعة ما في أحد المتاجر، أو حساب قيمة الفائدة البنكية، وفي الإحصاءات المتنوعة، كما يمكن من خلالها معرفة نسبة المصوّتين في الانتخابات، ووصف نسب الربح لمختلف الشركات والمحلات التجارية، واحتساب قيمة العمولة لكل موظف حسب نسبة مبيعاته، كما تصف الكثير من الملصقات على الملابس كمية المواد المستخدمة في تصنيعها على شكل نسب مئوية، وفي غيرها الكثير من المجالات.[١٢][١٣]
لمزيد من المعلومات حول تطبيقات النسبة المئوية يمكنك قراءة المقال الآتي: تطبيقات على النسبة المئوية.
لمزيد من المعلومات حول حساب نسبة الربح يمكنك قراءة المقال الآتي: كيف أحسب نسبة الربح.
أمثلة متنوعة على حساب النسبة المئوية
- المثال الأول: حوّل الرقم الآتي إلى نسبة مئوية: 4/5.[٨]
- الحل: يمكن تحويل هذا العدد إلى نسبة مئوية عن طريق ضرب كل من البسط والمقال بالعدد 20 لتحويل المقام إلى العدد 100؛ لينتج أن: (4/5)*(20/20)=80/100=80%.
- المثال الثاني: يبلغ عدد الطالبات في أحد الصفوف 75 طالبة، احسب النسبة المئوية للإناث في هذا الصف الذي يبلغ المجموع الكلي لطلابه 150 طالباً.[٨]
- الحل: نسبة الإناث في الصف=75/150×100%=50%.
- المثال الثالث:ما هو العدد الذي يمثل نسبة 150% من العدد 50.[١٠]
- الحل: 150% من 50=150/100×50=75.
- المثال الرابع: يبلغ عدد الطلاب في إحدى المدارس 2384 طالباً، تقدم منهم 75% طالباً لتقديم أحد الامتحانات، ولم يتمكن 25% طالباً منهم من اجتيازه، احسب عدد الطلاب الناجحين في هذا الامتحان.[١٠]
- الحل: عدد الطلاب الذين تقدموا لأداء الامتحان = 75/100 × 2384 = 1788 طالباً، نسبة الطلاب الناجحين= 100%-نسبة الطلاب غير الناجحين= 100%-25%=75%، وعليه عدد الطلاب الناجحين = 75/100 × 1788 = 1,341 طالباً.
- المثال الخامس: تناولت إحدى العائلات الطعام في أحد المطاعم ودفعت مبلغ 30 دولاراً مقابل ذلك، إضافة إلى نسبة 9.5% كضريبة للمبيعات، ونسبة 10% بدل خدمة في المطعم، احسب المبلغ الكلي الذي دفعته العائلة.[١٤]
- الحل: لحساب المبلغ الكلي يجب أولاً حساب المبالغ التي تم دفعها كبدل خدمة وكضريبة للمبيعات، وهي تساوي= 10/100 × 30=3 دولارات، 9.5/100 × 30 = 2.85 دولاراً، ثم حساب المبلغ الكلي، وهو يساوي 3+2.85+30=35.85 دولاراً.
- المثال السادس: استثمرت خلود مبلغاً من المال قدره 2000 دولاراً، بنسبة فائدة مركبة تبلغ 5% سنوياً، ولمدة خمس سنوات، احسب القيمة الكلية للفائدة في نهاية هذه المدة.[١٤]
- الحل: بتطبيق القانون: قيمة الفائدة المركبة= المبلغ الأصلي × (1+نسبة الفائدة السنوي)مدة القرض بالسنوات -المبلغ الأصلي=2000× (1+0.05)5-2000= 552.56 دولاراً
لمزيد من المعلومات حول الفائدة المركبة، وفائدة البنك يمكنك قراءة المقالات الآتية: كيف تحسب فائدة البنك، كيفية احتساب الفائدة المركبة.
- المثال السابع: إذا كان لدى هدى 30علبة، منها 12علبة زرقاء اللون، جد نسبة العلب الزرقاء.[١٥]
- الحل: لحساب نسبة العلب الزرقاء يمكن تطبيق القانون: النسبة المئوية= (القيمة/القيمة الكلية)×100%=(12/30)×100%=40%، وهي نسبة العلب الزرقاء.
- المثال الثامن: إذا اشترى محمد حقيبة مدرسية سعرها دون إضافة الضريبة هو 6.95$، وكانت القيمة الإجمالية للفاتورة بعد الشراء 7.61$، جد قيمة نسبة ضريبة المبيعات على البضائع في هذه المدينة.[١٦]
- الحل:
- يجب أولاً لحساب نسبة ضريبة المبيعات حساب قيمة الفرق في السعر بين القطعة بعد إضافة الضريبة إليها، وقبل إضافتها، لينتج أن: قيمة الضريبة= 7.61-6.95=0.66$.
- قسمة قيمة الضريبة على السعر الأصلي قبل إضافتها للحصول على نسبة ضريبة المبيعات: 0.66/6.95*100%=9.5%، وهي نسبة ضريبة المبيعات في هذه المدينة.
- المثال التاسع: إذا عملت سارة في متجر لبيع الأجهزة الكهربائية مقابل أجر يبلغ 8.5$ لكل ساعة عمل، إضافة إلى عمولة تبلغ نسبتها 4% مقابل كل عملية بيع تقوم بها، جد المبلغ الكلي الذي ستحصل عليه سارة بعد العمل لمدة يوم كامل، وتحقيق مبيعات قيمتها 1250$ في نهاية اليوم.[١٧]
- الحل:
- لمعرفة المبلغ الكلي يجب أولاً حساب قيمة أجرها الأصلي: وهو 8.5$ لكل ساعة عمل، وبما أنها عملت لمدة 7 ساعات فإن أجرها الإجمالي دون العمولة=8.5*7=59.5$.
- حساب قيمة العمولة التي ستحصل عليها سارة على مبيعاتها، وهي 4/100*1250=50$.
- حساب المبلغ الكلي الذي ستحصل عليه سارة في نهاية اليوم، وهو: 59.5+50=109.5$.
- المثال العاشر: حول الأعداد الآتية إلى نسب مئوية: 3/5، 37/40، 1/12.[١٨]
- الحل: يمكن تحويل هذا الأعداد إلى نسب مئوية عن طريق ضرب كل من البسط والمقال بالعدد المناسب لتحويل المقام إلى العدد 100؛ لينتج أن:
- 3/5=(3/5)*(20/20)=60/100=60%.
- 37/40=(37/40)*(2.5/2.5)=92.5/100=92.5%.
- 1/12=(1/12)*(8.33/8.33)=8.33/100=8.33%.
- المثال الحادي عشر: حول النسب المئوية الآتية إلى كسور: 37%، 125%، 10.5%.
- الحل: يمكن تحويل النسبة المئوية ببساطة إلى كسر عادي عن طريق وضع قيمة النسبة المئوية على مقام قيمته العدد 100، ثم تبسيط الكسر إلى أبسط صورة ممكنة، وذلك كما يأتي:[١٨]
- 37%=37/100.
- 125%=125/100=5/4.
- 10.5%=10.5/100=2.1/20=21/200.
- المثال الثاني عشر: أي الأعداد الآتية هو الأصغر: 0.18، 16%، 17/100.[١٨]
- الحل: لحل هذا السؤال يجب أولاً كتابة الأعداد على صورة واحدة لمقارنتها مع بعضها، وذلك كما يأتي:
- تحويل 0.18 إلى نسبة مئوية عن طريق ضرب هذا العدد فقط بالعدد مئة وإضافة علامة % إلى الناتج، وذلك 0.18*100=18%.
- تحويل 17/100 إلى نسبة مئوية عن طريق ضرب العدد الموجود في المقام برقم آخر مناسب لجعله مساوياً للعدد 100، وضرب البسط كذلك بنفس هذا العدد؛ وذلك للحفاظ على قيمة الكسر دون تغيير، إلا أن المقام في هذا المثال مساوٍ للعدد 100، مما يعني عدم ضرورة ضرب المقام والبسط بأي عدد، وبالتالي فإن 17/100=17%.
- مقارنة الأعداد السابقة ببعضها لينتج أن العدد الأصغر من بينها هو: 16%.
لمزيد من المعلومات حول حساب النسبة يمكنك قراءة المقال الآتي: كيف أحسب النسبة.
فيديو على كيفية حساب النسبة المئوية
للتعرف على كيفية حساب النسبة المئوية شاهد الفيديو:[١٩]
المراجع
- ↑ "The Meaning of Percent", www.mathgoodies.com, Retrieved 2-2-2019. Edited.
- ↑ "Percentages (%)", www.mathsisfun.com, Retrieved 1-4-2019. Edited.
- ↑ " Percent - a special type of fraction", extranet.education.unimelb.edu.au, Retrieved 1-4-2019. Edited.
- ↑ Mantci I., "What is a Percent? - Definition & Examples"، study.com, Retrieved 3-2-2020. Edited.
- ↑ "Calculating percentages", www.helpingwithmath.com, Retrieved 2-9-2018. Edited.
- ^ أ ب Yuanxin (Amy) Yang Alcocer, "Calculate Percentages: Formula & Overview"، www.study.com, Retrieved 30-10-2017.
- ^ أ ب ت ث Jon Zamboni (26-4-2018), "How to Change Any Number to a Percent, With Examples"، www.sciencing.com, Retrieved 1-4-2019. Edited.
- ^ أ ب ت "Percentage Formula", byjus.com, Retrieved 2-2-2020. Edited.
- ↑ "Introduction to Percentages %", www.skillsyouneed.com, Retrieved 2-2-2020. Edited.
- ^ أ ب ت .Ashish Siva, Manjunath Sreedaran, Yash Dev Lamba, and others, "Percentages"، www.brilliant.org, Retrieved 30-10-2017. Edited.
- ↑ "How to Multiply or Divide Two Percentages", www.wikihow.com, Retrieved 3-2-2020. Edited.
- ↑ "Ratio, proportion and percentages", www.open.edu, Retrieved 2-2-2020. Edited.
- ↑ "Everyday Use of Percentages", www.staff.vu.edu.au, Retrieved 1-4-2019. Edited.
- ^ أ ب "Percent Maths Problems", www.analyzemath.com, Retrieved 3-2-2020. Edited.
- ↑ Anne Marie Helmenstine, Ph.D. (6-2-2020), "www.thoughtco.com"، How to Calculate Percent, Retrieved 24-3-2020. Edited.
- ↑ "Basic "Percent of" Word Problems", www.purplemath.com, Retrieved 24-3-2020. Edited.
- ↑ "Percentages in the Real World Examples", www.shmoop.com, Retrieved 24-3-2020. Edited.
- ^ أ ب ت "Converting Fractions to Percents Exercises", www.shmoop.com, Retrieved 24-3-2020. Edited.
- ↑ فيديو على كيفية حساب النسبة المئوية.