محتويات

قانون محيط المستطيل عند معرفة أبعاده
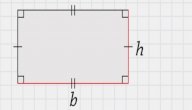
يُعّرف محيط المستطيل (بالإنجليزية: Perimeter of Rectangle) على أنه مجموع أطوال أضلاعه الأربعة، لكن من المعروف أن شكل المستطيل يمتاز بتساوي طول كل ضلعين متقابلين فيه، وهذا يعني أن محيطه يساوي ضعفي مجموع طوله وعرضه، وهو ما تعبر عنه المعادلة الحسابية الآتية:[١]
محيط المستطيل = 2 × (الطول + العرض)
وبالرموز: ح = 2 (ط + ع)، إذ إن:
- ح: محيط المستطيل.
- ط: الطول.
- ع: العرض.
مثال على حساب محيط المستطيل عند معرفة أبعاده
ما هو محيط المستطيل الذي طوله 76.2 سم وعرضه 15.24 سم؟[١]
- الحل:
- تكتب المعادلة الحسابية، محيط المستطيل = 2 × (الطول + العرض)، (ح = 2 (ط + ع)).
- يعوض المعطى في المعادلة مباشرةً؛ محيط المستطيل = 2 × (76.2 + 15.24)
- يحسب الناتج، محيط المستطيل = 182.88 سم.
قانون محيط المستطيل عند معرفة طول القطر وأحد الأبعاد
عند حساب محيط مستطيل معلوم القُطر يجب الاستعانة بنظرية فيثاغورس، لأن القطر يقسم المستطيل إلى مثلثين قائمي الزاوية، إذ تنص نظرية فيثاغورس؛ على أن "المثلث قائم الزاوية يكون فيه مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة"، ومن هذه النظرية يمكن معرفة بُعد المستطيل الثاني،[٢] لكن عند تعويض المعطيات في نص النظرية يمكن استنتاج معادلة بسيطة تربط بين محيط المستطيل وقطره، وهو ما تعبر عنه العلاقة الحسابية التالية:[٣]
محيط المستطيل = 2 × (طول الضلع + الجذر التربيعي لناتج طرح مربع الضلع من مربع القطر)
وبالرموز: ح = 2 (ض + (ق² - ض²)√)، إذ إن:
- ح: محيط المستطيل.
- ض: طول الضلع.
- ق: طول القُطر.
مثال على حساب محيط المستطيل عند معرفة طول القطر وأحد الأبعاد
جد محيط مستطيل طول قطره 25.40 سم وطول أحد أضلاعه 20.32 سم؟[٢]
- الحل:
- تكتب المعادلة الحسابية، محيط المستطيل = 2 × (طول الضلع + الجذر التربيعي لناتج طرح مربعي القُطر والضلع)، (ح = 2 (ض + (ق² - ض²)√)).
- يعوض المعطى في المعادلة مباشرةً؛ محيط المستطيل = 2 (20.32 + (²25.40 - ²20.32)√)
- يحسب الناتج، محيط المستطيل = 71.12 سم.
قانون محيط المستطيل عند معرفة المساحة وأحد الأبعاد
يمكن حساب محيط مستطيل ما عند معرفة مساحته (المساحة؛ هي الحيز الذي يشغله الشكل)، ويمكن التعبير عن مساحة المستطيل بالمعادلة الرياضية التالية: مساحة المستطيل = الطول × العرض، وبالرموز: م = ط × ع.[٣]
مما سبق نجد أن هنالك علاقة تربط بين محيط المستطيل ومساحته، وباستخدام كل من القانونين الرياضيين لمحيط المستطيل ومساحته يمكن اشتقاق قانون ثالث يربط بينهما، والذي يمكن التعبير عنه بالعلاقة الرياضية التالية:
محيط المستطيل = ((2 × مساحة المستطيل) + (2 × طول الضلع²))/ طول الضلع
وبالرموز: ح = ((2 × م) + (2 × ض²))/ ض، إذ إن:
- ح: محيط المستطيل.
- م: مساحة المستطيل.
- ض: طول الضلع.
مثال على حساب محيط المستطيل عند معرفة المساحة وأحد الأبعاد
جد محيط مستطيل مساحته 660 م2 وطول أحد أضلاعه 33 م؟[٤]
- الحل:
- تكتب المعادلة الحسابية، محيط المستطيل = ((2 × مساحة المستطيل) + (2 × طول الضلع²))/ طول الضلع، (ح = ((2 × م) + (2 × ض²))/ ض).
- يعوض المعطى في المعادلة مباشرةً؛ محيط المستطيل = ((2 × 660) + (2 × ²33))/ 33
- يحسب الناتج، محيط المستطيل = 106 م.
تتعدد قوانين محيط المستطيل باختلاف المعطيات، فلحساب محيط المستطيل عند معرفة أبعاده، تطبق العلاقة الرياضية التالية: محيط المستطيل = 2 × (الطول + العرض)، ولحساب محيط المستطيل عند معرفة طول القطر وأحد الأبعاد، تُطبق العلاقة الرياضية التالية المشتقة من نظرية فيثاغورس: محيط المستطيل = 2 × (طول الضلع + الجذر التربيعي لناتج طرح مربعي القُطر والضلع)، أما لحساب محيط المستطيل عند معرفة المساحة وأحد الأبعاد، تُطبق العلاقة الرياضية التالية: محيط المستطيل = ((2 × مساحة المستطيل) + (2 × طول الضلع²))/ طول الضلع.
المراجع
- ^ أ ب Joseph Vigil, "How to Find the Perimeter of a Rectangle: Formula & Example", Study.com, Retrieved 1/7/2021. Edited.
- ^ أ ب "How to Find the Area of a Rectangle Using the Diagonal", wikiHow, 16/6/2021, Retrieved 1/7/2021. Edited.
- ^ أ ب "Rectangle. Formulas and Properties of a Rectangle", OnlineMSchool, Retrieved 1/8/2021. Edited.
- ↑ "Perimeter and Area of Rectangle", Math-Only-Math.com, Retrieved 1/7/2021. Edited.