محتويات

قانون محيط المستطيل
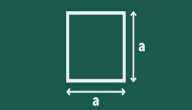
يمكن تعريف محيط المستطيل (بالإنجليزية:Perimeter of a Rectangle) على أنّه الطول الكلي لجميع أضلاع المستطيل، وبالتالي فهو يمثّل حاصل جمع كافة أضلاع المستطيل والتي يبلغ عددها 4 أضلاع،[١] ، ومحيط المستطيل يساوي حاصل جمع أطوال أضلاع المستطيل، ويمكن حساب محيط المستطيل من خلال تطبيق الصيغة التالية:
- المحيط= الطول+ الطول+ العرض+ العرض.
- وبما أنّ من خصائص المستطيل أنّ كل ضلعين متقابلين متساويين؛ فإنّ محيط المستطيل= 2 × العرض +2× الطول.
- ويؤخذ العدد 2 كعامل مشترك ليُصبح المحيط = 2 × (العرض + الطول).
- وبالرموز:[٢]ح = 2 (ع + ط)، حيثُ يمثّل:
- ح: محيط المستطيل.
- ع: عرض المستطيل.
- ط: طول المستطيل.
ويُمكن حساب المحيط بدلالة مساحته وأحد أضلاعه باستخدام الصيغة التالية:[٣]
- المحيط = ((2× المساحة) +(2× تربيع الضلع)) / الضلع، وبالرموز:
- ح =((2×م)+(2×ض²))/ ض،حيثُ يمثّل:
- ض: أحد أضلاع المستطيل.
المستطيل هو عبارة عن مضلع رباعي ومن خصائصه أنّ أضلاعه المتقابلة تكون متساوية، وبما أنّ المحيط بشكلٍ عام يُمثّل حاصل جمع كافة الجوانب، فإنَّ محيط المستطيل يُمكن حسابه من خلال الصيغة الرياضية؛ المحيط = 2 × (العرض + الطول)، و يُشار إلى أنّه من المهم تعلم حساب مساحة ومحيط كل من المستطيل والمربع كونهما من الأشكال الهندسية الأكثر شيوعًا.
قانون مساحة المستطيل
يُمكن تعريف مساحة المستطيل (بالإنجليزية:Area of a Rectangle) على أنّها مقدار المنطقة التي تشغل الحيّز داخل حدود أضلاع المستطيل،[٤] وبتعريف آخر هي عدد الوحدات المربّعة التي يُغطّيها المستطيل،[٥] إلّا أن القانون العام لحساب مساحة المستطيل يساوي حاصل ضرب طول المستطيل مع عرضه،[٦] ويُمكن كتابة قانون مساحة المستطيل كما يلي :[٤]
- المساحة = الطول × العرض، وبالرموز:
- م = ط × ع، حيثُ يمثّل:
- م: مساحة المستطيل.
- ط: طول المستطيل.
- ع: عرض المستطيل.
يُمكن كذلك حساب مساحة المستطيل بدلالة محيطه وأحد أضلاعه من خلال الصيغة الحسابية:[٣]
- المساحة = ((المحيط × الضلع) - (2× تربيع الضلع)) /2، وبالرموز؛
- م= ((ح×ض) - (2×ض²))/2،حيثُ يمثّل:
- ض: أحد أضلاع المستطيل.
أمثلة متنوعة على حساب محيط ومساحة المستطيل
يُدرج فيما يلي بعض الأمثلة المتنوعة لحساب محيط المستطيل في الحالات الآتية:
حساب محيط المستطيل إذا كان طول المستطيل وعرضه معلومين
- مثال1: جد محيط المستطيل الذي يبلغ طول ضلعه 12 سم، وعرضه 7 سم؟
- تكتب الصيغة الحسابية لمحيط المستطيل: ح= 2 × (ع + ط).
- تعويض القيم المعطاة في الصيغة مباشرةً: ح = 2 × (7 + 12)
- تُوجد القيمة بين الأقواس لأنّ الأولويّة للأقواس= 2 × 19= 38 سم.
- يساوي محيط المستطيل 38 سم.
- مثال2: جد محيط المستطيل الذي يبلغ طوله 9 إنش، وعرضه 7 إنش؟
- تكتب الصيغة الحسابية لمحيط المستطيل؛ ح= 2 (ع + ط).
- تعويض القيم المعطاة في الصيغة مباشرةً؛ ح= 2 (7 + 9)
- تُوجد القيمة بين الأقواس لأنّ الأولويّة للأقواس= 2 × 16= 32 إنش.
- يساوي محيط المستطيل 32 إنش.
- مثال3: جد محيط حديقة مستطيلة الشكل يبلغ طولها 10 متر وعرضها 3 أمتار؟
- تكتب الصيغة الحسابية لمحيط المستطيل: ح = 2 × (ع + ط).
- تعويض القيم المعطاة في الصيغة مباشرةً: ح = 2 × (3+ 10)
- تُوجد القيمة بين الأقواس لأنّ الأولويّة للأقواس= 2 × 13 = 26 متر.
- يساوي محيط الحديقة 26 متر.
- مثال4: ما هو محيط سجادة مستطيلة الشكل يبلغ طولها 25 سم، وعرضها 10 سم؟
- تكتب الصيغة الحسابية لمحيط المستطيل: ح = 2 × (ع + ط).
- تعويض القيم المعطاة مباشرةً: ح = 2 × (10+ 25)
- تُوجد القيمة بين الأقواس، لأنّ الأولويّة للأقواس= 2 × 35= 70سم.
- يساوي محيط السجادة 70 سم.
حساب المحيط عند معرفة المساحة وأحد الأضلاع
- مثال1: جد محيط المستطيل الذي تبلغ مساحته 24 سم مربع، وطول ضلعه 6 سم؟
- تكتب الصيغة الحسابية لمحيط المستطيل بدلالة المساحة؛ ح = ((2×م)+(2× ض²))/ ض.
- تعويض القيم المعطاة مباشرةً؛ ح =((2×24)+(2ײ6))/6=(48+72)/6= 120/6=20 سم.
- يساوي المحيط 20 سم.
- مثال2: ما هو محيط شاشة مستطيلة الشكل تبلغ مساحتها 36 إنش مربّع، وطول ضلعها 3 إنش؟
- تكتب الصيغة الحسابية لمحيط المستطيل بدلالة المساحة؛ح = ((2×م)+(2× ض²))/ ض.
- تعويض القيم المعطاة مباشرةً؛ ح =((2×36)+(2×3²))/3 =(72+18)/3= 90/3=30 إنش.
- يساوي محيط الشاشة 30 إنش.
حساب المساحة إذا كان طول المستطيل وعرضه معلومين
- مثال1: جد مساحة مزرعة يبلغ طولها 15 كم وعرضها 5 كم؟
- تكتب الصيغة الحسابية لمساحة المستطيل: م = ط × ع.
- تعويض القيم المعطاة مباشرةً: م =15× 5= 75 كم².
- تساوي مساحة المزرعة 75 كم مربع.
- مثال2: جد مساحة بركة السباحة التي يبلغ طولها 6 أمتار وعرضها 2 متر؟
- تكتب الصيغة الحسابية لمساحة المستطيل: م = ط × ع.
- تعويض القيم المعطاة مباشرةً: م = 6×2=12 م².
- تساوي مساحة البركة 12 م².
- مثال3: جد مساحة مستطيل طوله 5/2 سم وعرضه 1/2 سم؟
- تكتب الصيغة الحسابية لمساحة المستطيل؛ م= ط × ل.
- تعويض القيم المعطاة مباشرةً؛ م=5/2×1/2=5/4 سم².
- تساوي مساحة المستطيل 5/4 سم².
حساب المساحة عند معرفة المحيط وأحد الأضلاع
- مثال1: جد مساحة المستطيل الذي محيطه 40 سم وطول ضلعه 8 سم؟
- تكتب الصيغة الحسابية لمساحة المستطيل بدلالة المحيط: م = ((ح×ض) - (2× ض²))/2.
- تعويض القيم المعطاة مباشرةً؛ م=((40×8)-(2×8²))/2=(320-128)/2= 96 سم مربع.
- تساوي المساحة 96 سم مربع.
- مثال2: جد مساحة شاشة جهاز محيطها 32 إنش وطول أحد جوانبها 6 إنش؟
- تكتب الصيغة الحسابية لمساحة المستطيل بدلالة المحيط: م=((ح×ض) - (2×ض²))/2.
- تعويض القيم المعطاة مباشرةً: م=((32×6) - (2× 6²))/ 2= (192- 72)/2= 60 إنش².
- تساوي مساحة الشاشة 60 إنش².
الخلاصة
يُمكن حساب محيط المستطيل ومساحته من خلال المعطيات المتوفرة؛ حيثُ يُمكن حساب محيط المستطيل عند معرفة طوله وعرضه باستخدام الصيغة الحسابية التالية: محيط المستطيل =2 (العرض+ الطول)، ويُمكن حساب مساحته باستخدام الصيغة الحسابية التالية: المساحة = الطول × العرض.
المراجع
- ↑ "Perimeter Of A Rectangle - Definition with Examples", splashlearn, Retrieved 16/8/2021. Edited.
- ↑ "Perimeter of Rectangle", byjus, Retrieved 16/8/2021. Edited.
- ^ أ ب "Rectangle. Formulas and Properties of a Rectangle", onlinemschool, Retrieved 17/8/2021. Edited.
- ^ أ ب "Area of Rectangle", cuemath, Retrieved 16/8/2021. Edited.
- ↑ "How To Find The Area of a Rectangle Using Area of Rectangle Formula", mathgoodies, Retrieved 17/8/2021. Edited.
- ↑ "Area of rectangles review", khanacademy, Retrieved 17/8/2021. Edited.