محتويات

محيط المثلث
قانون حساب محيط المثلث
يمكن تعريف المحيط (بالإنجليزية: Perimeter) بأنه الطول الكلي لحدود الشكل الهندسي التي تُحيط به من الخارج، ويُقاس المحيط بعدد من الوحدات الطولية مثل المتر (م)، والسنتيمتر (سم)، والمليمتر (مم)،[١] ومحيط أي مثلث يُساوي مجموع أطوال أضلاعه، وبالتالي فإن:[٢]
- محيط المثلث متساوي الأضلاع = 3×أ، حيث أ: طول أحد اضلاع المُثلث.
- محيط المثلث متساوي الساقين = 2×أ+ب، حيث أ: طول أحد الضلعين المُتساويين، وب: طول قاعدة المثلث.
- محيط المثلث مختلف الاضلاع = أ+ب+ج، حيث أ، وب، وجـ هي أطوال الأضلاع الثلاث للمثلث.
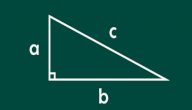
- محيط المثلث القائم = أ+ب+جـ = أ+ب+(أ²+ب²)√؛ حيث: [٣]
- أ، وب: هما ضلعا القائمة، ويمثلان ارتفاع المثلث القائم، وطول قاعدته.
- جـ: طول الوتر.
- تم الحصول على القانون السابق باستخدام نظرية فيثاغورس التي يمكن الاستعانة بها لإيجاد محيط المثلث القائم في الحالات التي لا يكون فيها أحد أضلاعه معروفاً، وذلك كما يلي:[٣]
- تنص نظرية فيثاغورس على أن مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر، أي: جـ² = أ² + ب²، وبالتالي فإن الوتر (جـ) = (أ²+ب²)√، وبالتعويض في قانون محيط المثلث القائم فإن المحيط = أ+ب+(أ²+ب²)√.
لمزيد من المعلومات والأمثلة حول محيط المثلث يمكنك قراءة المقالات الآتية: قانون محيط المثلث، كيفية حساب محيط المثلث القائم، قانون محيط المثلث متساوي الساقين
أمثلة على حساب محيط المثلث
- المثال الأول: حديقة مثلثة الشكل أطول أضلاعها 90م، و70م، و40م، يراد إحاطتها بسياج، فما هو طول السياج الذي يلزم لإحاطتها؟[٤]
- الحل: طول السياج = محيط المثلث، وبالتالي محيط المثلث = مجموع أطوال أضلاعه = 90+70+40= 200م.
- المثال الثاني: ما هو محيط المثلث الذي أطوال أضلاعه الثلاثة 5سم، و4سم، و2سم؟[٣]
- الحل: محيط المثلث = مجموع أطوال أضلاعه= 5+4+2= 11سم.
- المثال الثالث: ما هو محيط المثلث متساوي الأضلاع الذي طول أحد أضلاعه الثلاثة (أ) 10سم؟[٣]
- الحل: محيط المثلث متساوي الأضلاع = 3×أ= 3×10= 30 سم.
- المثال الرابع: إذا كان محيط المثلث متساوي الساقين 40سم، وطول أحد الضلعين المتساويين (أ) يساوي 10سم، فما هو طول قاعدة المثلث متساوي الساقين (ب)؟[٣]
- الحل: محيط المثلث متساوي الساقين= 2×أ+ب، وبالتعويض في هذا القانون فإن:
- 40= 2×10+ب، 40= 20+ب، ب= 20سم، وهو طول قاعدة المثلث.
- المثال الخامس: ما هو محيط المثلث القائم الذي ارتفاعه (أ) يساوي 4سم، وطول قاعدته (ب) يساوي 3سم؟[٣]
- محيط المثلث القائم = مجموع أطوال أضلاعه
- لإيجاد محيط المثلث فإنه يجب إيجاد الوتر (جـ) أولاً، وذلك كما يلي:
- جـ² = أ²+ب²= 3²+4²= 25، ومنه: جـ = 25√= 5سم.
- بعد إيجاد طول الوتر يمكن إيجاد محيط المثلث القائم كما يلي:
- محيط المثلث القائم = 4+3+5= 12سم.
- يمكن كذلك حساب المحيط مباشرة بالتعويض في القانون: محيط المثلث القائم = أ+ب+(أ²+ب²)√ = 3+4+(3²+4²)√= 12سم
- المثال السادس: ما هو محيط المثلث متساوي الأضلاع الذي ارتفاعه (ع) 10سم؟
- الحل:
- باستخدام نظرية فيثاغورس فإنه يمكن حساب طول ضلع المثلث (أ)؛ وذلك لأن الارتفاع هو العمود المقام من رأس المثلث متساوي الأضلاع إلى منتصف القاعدة، وبالتالي فإنه يشكّل مثلثاً قائم الزاوية الوتر فيه هو أحد الضلعين المتساويين (أ)، ومنتصف القاعدة (أ/2)، والارتفاع هما ضلعا القائمة، وذلك كما يلي:
- (طول أحد الضلعين المتساويين)²= (الارتفاع)²+(طول القاعدة/2)²، أ² = 10²+ (أ/2)²، 400+أ² = 4أ²، أ= 11.55 سم، وهو طول ضلع المثلث.
- بعد إيجاد طول أحد أضلاع المثلث متساوي الأضلاع فإنه يمكن إيجاد محيطه، وذلك كما يلي:
- محيط المثلث = 3×طول الضلع (أ) = 3 ×11.55 = 34.6 سم تقريباً
- المثال السابع: مثلث قائم الزاوية طول قاعدته 5 وحدات، وقياس الزاوية المحصورة بين الوتر، والقاعدة يساوي 28 درجة، فما هو محيط المثلث؟[٥]
- الحل: لحساب محيط المثلث يجب أولاً إيجاد الارتفاع، والوتر، وذلك لأن محيط المثلث= مجموع أطوال أضلاعه، وذلك كما يلي:
- إيجاد الارتفاع، وذلك كما يلي:
- يشكل الارتفاع الضلع المقابل للزاوية 28 درجة، والقاعدة هي الضلع المجاور لها، وعليه: ظا(28) = المقابل/المجاور، ومنه:
- 0.5317 = الارتفاع/5، ومنه: الارتفاع = 2.66 تقريباً.
- إيجاد الوتر باستخدام نظرية فيثاغورس، وذلك كما يلي:
- الوتر² = الارتفاع ² + طول القاعدة²، ومنه: الوتر= (2.66²+5²)√= 5.67 تقريباً.
- حساب محيط المثلث، وذلك كما يلي:
- محيط المثلث = 5+2.66+5.67 = 13.33 وحدة.
مساحة المثلث
قانون حساب مساحة المثلث
يمكن تعريف المساحة (بالإنجليزية: Area) بأنها كمية الفراغ المحجوز بواسطة الشكل ثنائي الأبعاد،[٤] وتُقاس بالوحدات المربعة،[١] ويمكن حساب مساحة المثلث باستخدام مجموعة من القوانين، وذلك بناءً على معطيات السؤال، وهي:[١]
- مساحة المثلث = (1/2)× طول القاعدة× الارتفاع، وبالرموز: مساحة المثلث= (1/2)×ق×ع؛ حيث:
- ق: طول قاعدة المثلث.
- ع: ارتفاع المثلث.
- مساحة المثلث= [س×(س-أ)×(س-ب)×(س-جـ)]√؛ حيث:
- أ، ب، جـ: أطوال أضلاع المثلث الثلاث.
- س: نصف محيط المثلث، وتساوي: س= (1/2)×(أ+ب+جـ).
- إذا عُلم قياس ضلعين وزاوية محصورة بينهما: مساحة المثلث= (أ×ب×جا س)/ 2: ، حيث:[٦]
- أ، وب: طول ضلعين من أضلاع المثلث.
- س: الزاوية المحصورة بين الضلعين أ،ب.
لمزيد من المعلومات والأمثلة حول مساحة المثلث يمكنك قراءة المقالات الآتية: كيف أحسب مساحة المثلث، قانون مساحة المثلث قائم الزاوية.
- مساحة المثلث متساوي الأضلاع = (3√×أ²)/4، حيث:
- أ: طول أحد أضلاع المثلث المتساوية.
لمزيد من المعلومات والأمثلة حول مساحة المثلث متساوي الأضلاع يمكنك قراءة المقال الآتي: قانون مساحة المثلث متساوي الأضلاع.
- مساحة المثلث متساوي الساقين= (1/4)×ب×(4×أ²-ب²)√، حيث:
- أ: طول أحد الضلعين المتساويين.
- ب: طول القاعدة، أو الضلع الثالث للمثلث متساوي الساقين.
لمزيد من المعلومات والأمثلة حول مساحة المثلث متساوي الساقين يمكنك قراءة المقال الآتي: قانون مساحة المثلث متساوي الساقين.
أمثلة على حساب مساحة المثلث
- المثال الأول: ما هي مساحة المثلث متساوي الأضلاع الذي ارتفاعه (ع) 10سم؟
- الحل: باستخدام نظرية فيثاغورس فإنه يمكن حساب طول ضلع المثلث (أ)؛ وذلك لأن الارتفاع هو العمود المقام من رأس المثلث متساوي الأضلاع إلى منتصف القاعدة، وبالتالي فإنه يشكّل مثلثاً قائم الزاوية الوتر فيه هو أحد الضلعين المتساويين (أ)، ومنتصف القاعدة (أ/2)، والارتفاع هما ضلعا القائمة، وذلك كما يلي:
- (طول أحد الضلعين المتساويين)²= (الارتفاع)²+(طول القاعدة/2)²، أ² = 10²+ (أ/2)²، 400+أ² = 4أ²، أ= 11.55 سم، وهو طول ضلع المثلث.
- بتعويض قيمة أ فإن مساحة المثلث متساوي الأضلاع = (3√×أ²)/4 = (3√×11.55²)/4 = 57.7 سم² تقريباً.
- الحل: باستخدام نظرية فيثاغورس فإنه يمكن حساب طول ضلع المثلث (أ)؛ وذلك لأن الارتفاع هو العمود المقام من رأس المثلث متساوي الأضلاع إلى منتصف القاعدة، وبالتالي فإنه يشكّل مثلثاً قائم الزاوية الوتر فيه هو أحد الضلعين المتساويين (أ)، ومنتصف القاعدة (أ/2)، والارتفاع هما ضلعا القائمة، وذلك كما يلي:
- المثال الثاني: ما هي مساحة المثلث حاد الزوايا الذي طول قاعدته 15 سم، وارتفاعه 4 سم؟[٧]
- الحل: مساحة المثلث = (1/2) × طول القاعدة × الارتفاع = (1/2) ×15× 4= 30 سم²
- المثال الثالث: ما هي مساحة المثلث قائم الزاوية الذي طول قاعدته 6 سم، وارتفاعه 9 سم؟[٧]
- الحل: مساحة المثلث = (1/2) × طول القاعدة × الارتفاع = (1/2)×6×9 = 27 سم²
- المثال الرابع: إذا كانت مساحة سجادة مثلثة الشكل تساوي 18م²، وطول قاعدتها 3م، فما هو ارتفاعها؟[٧]
- الحل:
- مساحة المثلث = (1/2)×طول القاعدة×الارتفاع، وبتعويض القيم في القانون ينتج أن:
- 18 = (1/2)×3×الارتفاع، وبضرب الطرفين بـ (2) فإن: 36= 3×الارتفاع، وبقسمة الطرفين على (3) فإن: الارتفاع = 12م.
- المثال الخامس: إذا كان المثلث أ ب جـ فيه قياس الزاوية (ب) 145 درجة، وقياس أب يساوي 4سم، وقياس ب جـ يساوي 3سم، فما هي مساحة المثلث؟[٨]
- الحل: مساحة المثلث= (1/2)×الضلع الأول×الضلع الثاني×جا (الزاوية المحصورة بينهما) = (1/2)×3×4×جا(145)= 3.44 سم²
- المثال السادس: مثلث قائم الزاوية طول قاعدته 5 وحدات، وقياس الزاوية المحصورة بين الوتر، والقاعدة يساوي 28 درجة، فما هي مساحة المثلث؟[٥]
- الحل:
- لحساب مساحة المثلث يجب أولاً إيجاد الارتفاع وذلك لأن مساحة المثلث= 1/2×طول القاعدة×الارتفاع، ولحساب الارتفاع يمكن اتباع ما يلي:
- يشكل الارتفاع الضلع المقابل للزاوية 28 درجة، والقاعدة هي الضلع المجاور لها، وعليه: ظا (28) = المقابل/ المجاور، ومنه:
- 0.5317 = الارتفاع/5، ومنه: الارتفاع = 2.66 تقريباً.
- مساحة المثلث = 1/2 × طول القاعدة × الارتفاع= (1/2)×5×2.66= 6.65 وحدة مربعة تقريباً.
- المثال السابع: مثلث طول قاعدته 7س، وارتفاعه 4س، فإذا كانت مساحته تساوي 28 وحدة مربعة، فما هو طول قاعدته، وارتفاعه؟[٥]
- الحل:
- مساحة المثلث= (1/2)×طول القاعدة×الارتفاع، وبالتعويض في هذا القانون فإن:
- 28=(1/2)×7س×4س، 28 = 14 س²، ومنه: س= 2√.
- طول القاعدة = 7 س = 2√7.
- الارتفاع = 4س = 2√4.
لمزيد من المعلومات والأمثلة حول المثلثات يمكنك قراءة المقال الآتي: بحث رياضيات عن المثلثات.
المراجع
- ^ أ ب ت "Area and Perimeter", www.math-only-math.com, Retrieved 20-4-2020. Edited.
- ↑ "Area and Perimeter of a Triangle", www.superprof.co.uk, Retrieved 20-4-2020. Edited.
- ^ أ ب ت ث ج ح "Perimeter of Triangle", byjus.com, Retrieved 20-4-2020. Edited.
- ^ أ ب "Area and Perimeter of Triangle", www.splashlearn.com, Retrieved 20-4-2020. Edited.
- ^ أ ب ت "Area and Perimeter of Triangles", www.algebralab.org, Retrieved 21-4-2020. Edited.
- ↑ "Area of a triangle - "side angle side" (SAS) method", www.mathopenref.com, Retrieved 20-4-2020. Edited.
- ^ أ ب ت "Area of a Triangle", www.mathgoodies.com, Retrieved 21-4-2020. Edited.
- ↑ "Finding the Area of a Triangle Using Sine", www.varsitytutors.com, Retrieved 21-4-2020. Edited.