محتويات

كيفية حساب مساحة المستطيل
يُمكن تعريف مساحة المستطيل (بالإنجليزية: Area of Rectangle) بأنّها المنطقة التي يشغلها شكل المستطيل على سطح مستوٍ، وتُقاس بالوحدة المربعة،[١] كما يمكن حساب مساحة الأشكال الهندسية جميعها ومن بينها المستطيل، وتُحسب مساحته بعدة طرق وهي كالتالي:[٢]
مساحة المستطيل بمعلومية أبعاده
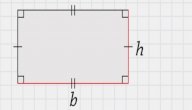
يتكوّن المستطيل من 4 زوايا قائمة و4 أضلاع، إذ تختلف أطوال أضلاعه بحيث له طول وعرض، أي ضلعين لهما نفس قيمة الطول وضلعين لهما نفس قيمة العرض، ويُمكن حساب مساحة المستطيل مختلف الأضلاع بالقانون التالي:
مساحة المستطيل= الطول × العرض، ويُكتب القانون بالرموز كالتالي:
م = س × ص؛ حيث أنّ:
- م: مساحة المستطيل.
- س: طول المستطيل.
- ص: عرض المستطيل.
ويمكن أن تكون المساحة معلومة ويُطلب من السؤال إيجاد الطول أو العرض، نستخدم نفس القانون لإيجاد المطلوب.
مساحة المستطيل بمعلومية قطره وأحد أبعاده
ولحساب مساحة المستطيل حسب الأقطار وعند معلومية أحد أبعاده يُمكن استخدام القانون التالي:[٣]
حساب عرض المستطيل إذا كانت قيمة القطر والطول معلومتين
- القطر² = الطول² + العرض².
- العرض√ = (القطر² - الطول²) √
- نعوض قيمة العرض في قانون المساحة:
- مساحة المستطيل=الطول×العرض.
- مساحة المستطيل = الطول × (القطر² - الطول²) √
حساب الطول إذا كانت قيمة القطر والعرض معلومتين
- القطر² = الطول² + العرض².
- الطول = (القطر² - العرض²) √
- نعوض قيمة الطول في قانون المساحة:
- مساحة المستطيل=الطول×العرض.
- مساحة المستطيل = (القطر² - العرض²) √ × العرض.
مساحة المستطيل بمعلومية محيطه
عند معرفة أحد أبعاد المستطيل ومحيطه في هذه الحالة لا بد من استخدام قانون محيط المستطيل لإيجاد الحل وإيجاد المساحة وذلك بالخطوات التالية:[٤]
على سبيل المثال: إذا كان محيط المستطيل يساوي 30 سم، وعرضه 5 سم، كم تبلغ مساحته؟
محيط المستطيل= 2 × (الطول + العرض)
- نعوض قيمة المحيط وقيمة العرض في القانون لإيجاد قيمة الطول المجهولة.
- محيط المستطيل= 2 × (الطول + العرض)
- 30 = 2 × (الطول + 5)
- 30= 2 × الطول + 2 × 5
- 30 = 2 × الطول + 10
- 20 = 2 × الطول
- الطول = 10 سم.
- مساحة المستطيل= الطول × العرض.
- مساحة المستطيل= 10 × 5.
- مساحة المستطيل= 50 سم².
الخلاصة:
مساحة المستطيل هي المنطقة التي يشغلها المستطيل على سطح مستوٍ، ويتميّز المستطيل أنّه مختلف الأضلاع وله بعدين وهما الطول والعرض، كما أنّ كل ضلعين متقابلين متساويين.
ويُمكن حساب مساحته بالقانون العام وهو الطول ضرب العرض، ولكن هناك حالات يكون أحد البعدين مجهول ويكون قطره معلوم فإنّنا نستخدم قانون فيثاغورس لإيجاد البعد الثاني، ثم إيجاد المساحة، أو استخدام قانون المحيط إذا كانت قيمته معلومة لإيجاد البعد المجهول، ثم حساب المساحة.
مسائل متنوعة على حساب مساحة المستطيل
تاليًا أمثلة مختلفة على حساب مساحة المستطيل.
إذا كانت أبعاده معلومة
احسب مساحة المستطيل إذا علمتَ أنّ طوله 8 سم وعرضه 4 سم.
الحل:
- مساحة المستطيل= الطول × العرض.
- مساحة المستطيل= 8 × 4.
- مساحة المستطيل= 24 سم².
احسب مساحة المستطيل إذا علمتَ أنّ طوله 10 سم وعرضه 7 سم.
الحل:
- مساحة المستطيل= الطول × العرض.
- مساحة المستطيل= 10 × 7.
- مساحة المستطيل= 70 سم².
إذا كان قطره وأحد أبعاده معلومين
احسب مساحة المستطيل إذا علمتَ أنّ قطره 5 سم وعرضه 3 سم.
الحل:
- القطر² = الطول² + العرض².
- 5² = الطول² + 3²
- 25 = الطول² + 9
- الطول = (25 - 9) √
- الطول = 16 √
- الطول = 4 سم.
- نعوض قيمة الطول في قانون المساحة:
- مساحة المستطيل=الطول×العرض.
- مساحة المستطيل = 4 × 3
- مساحة المستطيل = 12 سم².
احسب مساحة المستطيل إذا علمتَ أنّ قطره 8 سم وطوله 7 سم.
الحل:
- القطر² = الطول² + العرض².
- 8² = 7² + العرض²
- 64 = 49 + العرض²
- العرض = (64 - 49) √
- العرض = 15 √
- العرض = 3.87 سم.
- نعوض قيمة العرض في قانون المساحة:
- مساحة المستطيل=الطول×العرض.
- مساحة المستطيل = 7 × 3.87
- مساحة المستطيل = 27.09 سم².
إذا كان محيطه معلومًا
احسب مساحة المستطيل إذا علمتَ أنّ محيطه 16 سم وعرضه 2 سم.
الحل:
- محيط المستطيل= 2 × (الطول + العرض)
- 16 = 2 × (الطول + 2)
- 16= 2 × الطول + 2 × 2
- 16 = 2 × الطول + 4
- 12 = 2 × الطول
- الطول = 6 سم.
- مساحة المستطيل= الطول × العرض.
- مساحة المستطيل= 6 × 2.
- مساحة المستطيل= 12 سم².
فيديو عن كيفية حساب مساحة المستطيل
للتعرف على المزيد من المعلومات حول كيفية حساب مساحة المستطيل شاهد الفيديو: فيديو عن كيفية حساب مساحة المستطيل.فيديو عن كيفية حساب مساحة المستطيل.المراجع
- ↑ "Area of Rectangle", cuemath, Retrieved 23/8/2021. Edited.
- ↑ "Area of a Rectangle Calculator", omnicalculator, Retrieved 23/8/2021. Edited.
- ↑ "Area of Rectangle", byjus, Retrieved 23/8/2021. Edited.
- ↑ "Perimeter and Area of Rectangle", math-only-math, Retrieved 23/8/2021. Edited.