محتويات

قانون مساحة المكعب
بما أن المكعب يتكون من أوجه مربعة الشكل، فمن المهم معرفة كيفية حساب مساحة المربع للتوصّل من خلالها إلى قانون مساحة المكعب. والمربع (بالإنجليزية: Square) هو شكل هندسي يُعد حالة خاصّة من المستطيل، إذ إنه مستطيلٌ جميع أضلاعه متساوية في الطول، ولإيجاد مساحة المستطيل يتم إيجاد حاصل ضرب الطول (الضلع الأطول) * العرض (الضلع الأقصر)، وبما أن أطوال أضلاع المربع متساوية فإن الطول يساوي العرض، وبالتالي يمكن الحصول على مساحة المربع بإيجاد حاصل ضرب الضلع في نفسه، أي بتربيعه،[١] وبالرموز:
- مساحة المستطيل = س * ص
- حيث إن: س= الطول، ص= العرض
- بما أن س = ص في المربع إذن:
- مساحة المربع = س * س = س²
- حيث إن: س= طول ضلع المربع
أما بالنسبة لمساحة المكعب فيمكن حسابها عن طريق حساب مجموع مساحات أوجه المكعب،[١] وتُقسم مساحة المكعب إلى نوعين:
- مساحة المكعب الكلية: (بالإنجليزيّة: TotalSurface Area)، هي مجموع مساحات جميع الوجوه الستة، وبما أن هذه المربعات متطابقة تماماً فيمكن حساب مساحة أحد هذه المربعات وضرب المساحة الناتجة في العدد 6 (الذي يُشير إلى عدد أوجه المكعب)، بالتالي يمُكن إيجاد مساحة مكعب طول ضلعه س من خلال القانون:[١]
- مساحة المكعب = 6 * س²
- حيث إن س: طول ضلع المكعب
- مساحة السطح الجانبي للمكعب: (بالإنجليزية: Lateral Surface Area)، هي مجموع مساحات أوجه المكعب باستثناء الوجهين العلوي والسفلي، إذ يُمكن إيجاده من خلال القانون الآتي:[٢]
- مساحة السطح الجانبي للمكعب = 2 (س*س + س*س)
- مساحة السطح الجانبي للمكعب = 2(س² + س²)
- مساحة السطح الجانبي للمكعب = 2(2 س²)
- مساحة السطح الجانبي للمكعب = 4*س²
أمثلة على حساب مساحة المكعب
فيما يأتي بعض الأمثلة التي توضح كيفية حساب مساحة المكعب:[٣]
- مثال1: جد مساحة مكعب طول ضلع أحد أضلاعه 3 سم.
- الحل:
- بتطبيق قانون مساحة المكعب:
- مساحة المكعب = 6 * س²
- بتعويض طول الضلع 3 سم في القانون:
- مساحة المكعب = 6 * 3²
- مساحة المكعب = 6 * 3* 3
- مساحة المكعب = 54 سم²
- مثال2: أحسب مساحة مكعب اذا كان طول أحد أضلاعه 5سم.
- الحل:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * 5²
- مساحة المكعب = 6 * 5 * 5
- مساحة المكعب = 150 سم²
- مثال3: جد مساحة مكعب طول أحد أضلاعه 1/2 سم.
- الحل:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * (1/2)²
- مساحة المكعب = 6 * 1/4
- مساحة المكعب = 6 ÷ 4
- مساحة المكعب = 3 ÷ 2
- مساحة المكعب = 1.5 سم²
- مثال4: مكعب طول ضلعه 7سم، احسب مساحته الكلية.[٤]
- الحل:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * 7²
- مساحة المكعب = 294 سم²
- مثال5: جد مساحة مكعب طول احد أضلاعه 7.2 إنش.[٤]
- الحل:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * (7.2)²
- مساحة المكعب = 311.04 إنش²
- مساحة المكعب = 311 إنش² تقريباً
- مثال6: مكعب طول ضلعه 3 ÷ 2 ، احسب مساحته.
- الحل:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * (3 ÷ 2)²
- مساحة المكعب = 6 * 9 ÷ 4
- مساحة المكعب = 54 ÷ 4 = 13.5
- مثال7: أوجد النسبة بين المساحة الكلية ومساحة السطح الجانبي للمكعب.[٥]
- الحل:
- المساحة الكلية للمكعب = 6 * س²
- مساحة السطح الجانبي للمكعب = 4 * س²
بالقسمة:
- المساحة الكلية للمكعب ÷ مساحة السطح الجانبي للمكعب
- النسبة = 6 * س² ÷ 4 * س²
- النسبة = 6 ÷ 4
- النسبة = 3 ÷ 2
- إذن النسبة بين المساحة الكلية ومساحة السطح الجانبي للمكعب = 3 ÷ 2
حساب مساحة المكعب من حجمه
يمكن حساب مساحة المكعب عند معرفة قيمة حجمه، علماً بأن حجم المكعب = س³، حيث: س= طول ضلع المكعب،[٦] ولإيجاد مساحة المكعب في هذه الحالة يُمكن اتباع الخطوات الآتية:[٧]
- حساب طول ضلع المكعب من الحجم من خلال التعويض في قانون الحجم وإيجاد الجذر التكعيبي للحجم المُعطى، ويكون ذلك إمّا باستخدام الآلة الحاسبة أو من خلال البحث عن رقم يتم ضربه بنفسة ثلاث مرات فتنتج قيمة الحجم.
- بعد معرفة طول ضلع المكعب يتم تطبيق قانون مساحة المكعب وإيجاد المساحة، في ما يأتي مثال على ذلك:
- احسب مساحة مكعب إذا علمت أن حجمه يساوي 125 سم³.[٧]
- الحل:
- إيجاد طول الضلع من الجذر التكعيبي للحجم المُعطى 125، والذي يساوي 5، وذلك لأن 5 * 5 * 5 = 125، كما يمكن إيجاد طول الضلع من قانون الحجم:
- حجم المكعب = س³
- وبتعويض حجم المكعب
- 125 = س³
- وبأخذ الجذر التكعيبي للطرفين ينتج أن:
- طول الضلع س = 5
- تطبيق قانون مساحة المكعب:
- مساحة المكعب = 6 * س²
- مساحة المكعب = 6 * 5²
- مساحة المكعب = 150 سم²
حساب طول ضلع المكعب من مساحته
إذا كانت قيمة مساحة المكعب معلومة، فيمكن إيجاد طول ضلع المكعب عن طريق إعادة ترتيب قانون المساحة كالآتي:[٨]
- مساحة المكعب = 6 * س²
- بالقسمة على 6 للطرفين:
- مساحة المكعب ÷ 6 = س²
- بأخذ الجذر التربيعي للطرفين نتوصل إلى:
- س = (المساحة ÷ 6)√
- حيث إن س= طول ضلع المكعب
- مثال1: مكعب مساحته 96 سم²، أحسب طول ضلعه.[٤]
- الحل:
- مساحة المكعب = 6 * س²
- 96 = 6 * س²
- بالقسمة على 6 :
- 16 = س²
- بأخذ الجذر التربيعي للطرفين:
- س = +4 ، س= -4، وبما أن الطول لا يمكن أن يكون قيمته سالبة نتجاهل س = -4 وينتج أن:
- طول ضلع المكعب = 4 سم
- مثال2: جد طول ضلع مكعب إذا علمت أن مساحته تساوي 384 سم².[٩]
- الحل: مساحة المكعب = 6 * س²
- 384 = 6 * س²
- بالقسمة على 6 :
- 64 = س²
- بأخذ الجذر التربيعي للطرفين:
- س = +8 ، س= -8، وبما أن الطول لا يمكن أن يكون قيمته سالبة نتجاهل س = -8 وينتج أن:
- طول ضلع المكعب = 8 سم
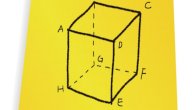
تعريف المكعب
يُعرّف المكعب (بالإنجليزيّة: Cube) في الهندسة الإقليدية بأنه مُجسّم صلب منتظم الشكل، يتكوّن من ستة أوجه، وهي عبارة عن مربعات متطابقة ترتبط معاً لتُشكل كل من الحواف والقِمم، ويعد المكعب -أو ما يّسمى بسداسي الأوجه (بالإنجليزيّة: hexahedron)- من المجسّمات الخمسة التي يُطلق عليها المواد الصلبة الأفلاطونية،[١٠][٦] وهو مصطلح يُطلق على الجسم الذي تكون كل أوجهه مضلعة، ومنتظمة، ومتماثلة.[١١]
أجزاء المكعب
يتكوّن المكعب من خمسة أجزاء وهي:[٦]
- الوجه (الجانب): (بالإنجليزية: Face)، فالمكعب يتكون من ستة أوجه مربعة الشكل، ولكل وجه أربعة أطوال متساوية وأربع زوايا داخلية قائمة.
- الحافة: (بالإنجليزية: Edge)، يتكون المكعب من اثنتي عشرة حافة أو ضلعاً متساوية في الطول، والحافة عبارة عن خط ينتج من التقاء رأسين معاً.
- الرأس: (بالإنجليزية: Vertex)، لكل مكعب ثمانية رؤوس، وهي عبارة عن نقطة تتشكل عند التقاء ثلاثة حواف معاً.
- القطر ثنائي الأبعاد: (بالإنجليزية: Face diagonals)، يتكون المكعب من اثني عشر قطراً، وهو عبارة عن خط يصل الرؤوس المتعاكسة في كل وجه، ويمكن حسابه من خلال القانون:
- قطر الوجه = (2*س²)√
- حيث إنّ س طول الوجه الواحد (الضلع)
- القطر ثلاثي الأبعاد: أو القطر الفضائي (بالإنجليزية: Space diagonals)، فلكل مكعب 4 أقطار داخلية، وهي عبارة عن خط يربط الزوايا أو الرؤوس المتعاكسة للمكعب من الداخل، فهو يصل بين ركنين متعاكسين قاطعاً الداخل للمكعب، ويمكن حسابه من خلال القانون:
- القطر الفضائي = (3* س²)√
- حيث س طول الوجه الواحد (الضلع)
خصائص المكعب
للمكعب عدد من الخصائص أهمها:[٦]
- كل وجه من أوجه المكعب يرتبط مع أربعة أوجه أخرى.
- جميع زوايا سطح المستوى هي زوايا قائمة وقياسها 90 درجة.
- تتكون الرؤوس من التقاء ثلاثة أضلع معاً.
- الحواف المتقابلة في كل وجه تتوازى مع بعضها البعض.
فيديو عن كيفية حساب حجم المكعب
للتعرف على كيفية حساب حجم المكعب شاهد الفيديو.[١٢]
المراجع
- ^ أ ب ت Chris Deziel (28-4-2018), "How to Calculate the Area of a Cube"، sciencing.com, Retrieved 23-10-2019. Edited.
- ↑ "Cuboid And Cube", byjus.com, Retrieved 23-10-2019. Edited.
- ↑ "Surface area of a cube", www.basic-mathematics.com, Retrieved 24-10-2019. Edited.
- ^ أ ب ت "High School Math : How to find the surface area of a cube", www.varsitytutors.com, Retrieved 24-10-2019. Edited.
- ↑ "Surface Area of Cube", www.ask-math.com, Retrieved 24-10-2019. Edited.
- ^ أ ب ت ث "Cube", www.mathopenref.com, Retrieved 23-10-2019. Edited.
- ^ أ ب "How to Find the Surface Area of a Cube", www.wikihow.com,5-5-2019، Retrieved 24-10-2019. Edited.
- ↑ " Surface area of a cube", www.mathopenref.com, Retrieved 23-10-2019. Edited.
- ↑ "What is the length of the side of a cube whose surface area is 384 ", www.enotes.com, Retrieved 24-10-2019. Edited.
- ↑ "Cube", www.britannica.com, Retrieved 23-10-2019. Edited.
- ↑ J.L. Heilbron, "Platonic solid"، www.britannica.com, Retrieved 28-10-2019. Edited.
- ↑ فيديو عن كيفية حساب حجم المكعب.