محتويات

قانون حساب مساحة سطح الكرة
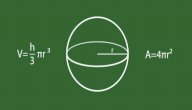
اكتُشفت صيغة قانون مساحة سطح الكرة منذ ألفيّ عام على يد الفيلسوف اليوناني أرخيميدس (بالإنجليزية: Archemedes)، حيثُ وجد أنّ مساحة سطح الكرة تساوي مساحة الجدار المنحني لأصغر اسطوانة بإمكانها أن تحتوي الكرة، كما أنّ مساحة سطح الكرة تساوي أربعة أضعاف مساحة الدائرة التي لها نفس نصف القطر (مساحة الدائرة= π×نق²)، وعليه يمكن حساب مساحة سطح الكرة باستخدام القانون الآتي:[١]
مساحة سطح الكرة= 4×π×نق²
حيثُ أنّ:
- نق: نصف قطر الكرة.
- π: باي، ثابت عددي قيمته 3.14 أو 22/7.
كما يُمكن ايجاد مساحة السطح المنحني لنصف الكرة من خلال القانون الآتي:[٢]
مساحة السطح المنحني لنصف الكرة =½×4×π×نق²= 2×π×نق²
ولأن نصف الكرة يتكوّن من سطحين؛ الأول الجزء المُنحني والآخر هو القاعدة المُسطحة الدائريّة، فإنّ إيجاد المساحة الكليّة لسطح نصف الكرة يتطلب جمع مساحة السطح المُنحني مع مساحة القاعدة المُسطّحة الدائريّة، لينتج أنّ:[٢]
المساحة الكليّة لسطح نصف الكرة=2×π×نق²+ π×نق²= 3×π×نق².[٢]
أمثلة على حساب مساحة سطح الكرة
وفيما يأتي أمثلة متنوعة على حساب مساحة سطح الكرة:
- المثال الأول: جد مساحة سطح كرة يبلغ طول نصف قطرها 5.5 م؟[٣]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 5.5 م في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×5.5²=379.94 م².
- المثال الثاني: كرة مساحتها تساوي 2464 سم²، جد نصف قطرها لأقرب منزلتين عشريّتين؟[٣]
- الحل:
- تعويض قيمة مساحة الكرة التي تساوي 2464 سم² في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: 2464=4×3.14×نق²، وبقسمة الطرفين على 4، ينتج أنّ: 616=3.14×نق²، ثمّ بقسمة الطرفين على 3.14، ينتج أنّ: نق²=196.17، ثمّ بأخذ الجذر التربيعيّ للطرفين، ينتج أنّ: نق= 14.00 سم.
- المثال الثالث: نصف كرة يبلغ نصف قطرها 8.3 سم، جد المساحة السطحية لنصف الكرة دون القاعدة الدائريّة؟[٣]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 8.3 سم في قانون مساحة السطح المنحني لنصف كرة = 2×π×نق²، ومنه ينتج أنّ: مساحة السطح المنحني لنصف كرة = 2×3.14×8.3²=432.6 سم².
- المثال الرابع: جد قيمة المساحة لسطح كرة يبلغ طول نصف قطرها 6سم؟[٣]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 6 سم في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×6²=452.16 سم².
- المثال الخامس: كرة يبلغ نصف قطرها 3 سم، جد مساحتها السطحيّة؟[٤]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 3 سم في قانون مساحة سطح الكرة= 4×π×نق²
- ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×3²=113.04 سم².
- المثال السادس: كرة يبلغ حجمها 36π وحدة حجم، جد مساحتها السطحيّة؟[٤]
- الحل:
- حساب قيمة نصف القطر (نق) بتعويض قيمة حجم الكرة في قانون حجم الكرة= 4/3×π×نق³، لينتج أنّ: 36 π×4/3=π×نق³، وبقسمة الطرفين على π، ينتج أنّ: 36=4/3×نق³، ثمّ بقسمة الطرفين على 4/3، ينتج أنّ: نق³=27، وبأخد الجذر الكعيبيّ للطرفين، ينتج أنّ: نق=3 وحدة.
- تعويض قيمة نصف القطر التي تساوي 3 سم في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×3²=113.04 سم².
- المثال السابع: ثمرة بطيخ كرويّة الشكل يبلغ حجمها 288π سم³، إذا قُسمت لنصفين مُتساويين، جد المساحة السطحيّة لنصف ثمرة البطيخ؟[٤]
- الحل:
- حساب قيمة نصف القطر (نق) بتعويض قيمة حجم الكرة في قانون حجم الكرة= 4/3×π×نق³، لينتج أنّ: نق³×288π =4/3×π، وبقسمة الطرفين على π، ينتج أنّ: 216=نق³، وبأخد الجذر الكعيبيّ للطرفين، ينتج أنّ: نق=6سم.
- تعويض قيمة نصف القطر التي تساوي 6سم في قانون مساحة نصف الكرة: المساحة الكليّة لسطح نصف الكرة= 3×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 3×3.14×6²=339سم².
- المثال الثامن: احسب تكلفة دهان سطح كرة يبلغ نصف قطرها 7 سم، إذا كان ثمن الدهان يساوي 2.5 قرش/سم²؟[٥]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 7 سم في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×7²=615.44 سم².
- حساب تكلفة دهان سطح الكرة بضرب مساحتها بالتكلفة؛ لينتج أنّ: 615.44×2.5=1538.6 قرشاً.
- المثال التاسع: كرة يبلغ نصف قطرها 5سم، جد مساحتها السطحيّة؟[٦]
- الحل:
- تعويض قيمة نصف القطر التي تساوي 5سم في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×5²=314سم².
- المثال العاشر: كرة مساحتها تساوي 16πسم²، جد حجمها؟[٧]
- الحل:
- حساب قيمة نصف القطر (نق) بتعويض قيمة مساحة الكرة التي تساوي 16πسم² في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: نق²×16π = 4×π، وبقسمة الطرفين على (4π) ينتج أن: نق²=4، ثمّ بأخذ الجذر التربيعيّ للطرفين، ينتج أنّ: نق= 2سم.
- تعويض نصف قطر الكرة في قانون حجم الكرة= 4/3×π×نق³، لينتج أنّ: حجم الكرة =4/3×3.14×2³= 33.5 سم³.
- المثال الحادي عشر: يبلغ محيط أكبر دائرة تحيط بكرة ما 13.8π سم، ما هي مساحة سطح الكرة؟[٨]
- حساب قيمة نصف القطر (نق) بالتعويض في قانون محيط الدائرة= π2نق، ومنه ينتج أنّ: π2نق=13.8π ، وبقسمة الطرفين على π2، ينتج أنّ: نق= 6.9 سم.
- تعويض قيمة نصف القطر التي تساوي 6.9 سم في قانون مساحة سطح الكرة= 4×π×نق²، ومنه ينتج أنّ: مساحة سطح الكرة= 4×3.14×6.9²= 597.9 سم².
نظرة عامة حول مساحة سطح الكرة
تُعرّف الكُرة (بالإنجليزية: Sphere) على أنّها جسم صلب ثلاثيّ الأبعاد له بنية مستديرة مثل الدائرة، إلا أن الدائرة ثُنائيّة الأبعاد بينما الكرة ثلاثيّة الأبعاد، وتُعرّف مساحة سطح الكرة (بالإنجليزية: Sphere Surface Area) على أنّها مقدار المنطقة التي يغطيها سطح الكرة.[٥]
وبما أنّ الكرة شبيهة بالدائرة فإن جميع النقاط الموجودة على سطحها تبعُد مسافة ثابتة عن مركزها، وتعرف هذه المسافة الثابتة بنصف قطر الكرة (بالإنجليزية: Radius)، ويمكن تعريف أطول مسافة مستقيمة داخل الكرة بقطر الكرة (بالإنجليزية: Diameter)، وبشكل عامّ إذا قُسم هذا الشكل الهندسيّ إلى نصفين فإن كل قسم منهما يُطلق عليه اسم نصف كرة (بالإنجليزية: Hemisphere).[٣]
المراجع
- ↑ "Surface area of a sphere", www.mathopenref.com, Retrieved 27-3-2020. Edited.
- ^ أ ب ت "sphere", www.toppr.com, Retrieved 27-3-2020. Edited.
- ^ أ ب ت ث ج "Surface Area of a Sphere", www.web-formulas.com, Retrieved 27-3-2020. Edited.
- ^ أ ب ت Worranat Pakornrat, Thaddeus Abiy, Geoff Pilling, and others, "Surface Area of a Sphere"، www.brilliant.org, Retrieved 27-3-2020. Edited.
- ^ أ ب "surface-area-of-a-sphere", www.byjus.com, Retrieved 27-3-2020. Edited.
- ↑ "Finding the Volume and Surface Area of a Sphere", www.ducksters.com, Retrieved 27-3-2020. Edited.
- ↑ "How to find the surface area of a sphere", www.varsitytutors.com, Retrieved 27-3-2020. Edited.
- ↑ "SURFACE AREA AND VOLUME OF SPHERES", www.onlinemath4all.com, Retrieved 27-3-2020. Edited.