محتويات

الخصائص العامة للمثلثات
يُمكن تعريف المثلث (بالإنجليزية: Triangle) على أنّه مُضّلع له ثلاثة أضلاع، وثلاث زوايا، وثلاث رؤوس،[١] ويُمكن تلخيص أهمّ خصائص المُثلث العامّة على النحو الآتي:[٢]
- مجموع زوايا المُثلث الثلاثة يساوي 180 درجة.
- مجموع طول أيّ ضلعين من أضلاع المُثلث أكبر من طول الضلع الثالث.
- الفرق بين طول أيّ ضلعين من أضلاع المُثلث أقلّ من طول الضلع الثالث.
- الضلع المُقابل للزاوية الكبرى في المُثلث هو الضلع الأطول.
- الزاوية الخارجية للمثلث تساوي مجموع الزاويتين الداخليّتين البعيدتين، وتُعرف هذه الخاصية باسم (خاصية الزاوية الخارجية).
- يتشابه المثلثان إذا كانت الزوايا المتقابلة لكل من المثلثين مُتطابقة وأطوال أضلاعهما مُتناسبة.
- قانون مساحة المثلث ومحيط المثلث هما النحو الآتي:
- مساحة المثلث=½×القاعدة×الارتفاع.
- محيط المثلث =مجموع جميع أضلاعه الثلاثة.
- يُعرف المُثلث الذي يكون قياس جميع زواياه أقل من 90 درجة بالمُثلث حادّ الزوايا (بالإنجليزية: Acute angle triangle).[١]
- يُعرف المُثلث الذي يمتلك زاوية واحدة قياسها أكبر من 90 درجة بالمُثلث مُنفرج الزاوية (بالإنجليزية: Obtuse angle triangle).[١]
لمزيد من المعلومات حول المثلثات يُمكنك قراءة المقالات الآتية: بحث رياضيات عن المثلثات، بحث عن تشابه المثلثات، انواع المثلثات، حساب زوايا المثلث.
لمزيد من المعلومات حول كيفية حساب مساحة ومحيط المثلث يُمكنك قراءة المقالات الآتية: كيف أحسب مساحة المثلث، قانون محيط المثلث
خصائص متوسط المثلث
يُعرف خطّ المتوسط للمُثلث (بالإنجليزية: Median of Triangle) على أنّه الخطّ المُمتد من إحدى الزوايا إلى مُنتصف الضلع الذي يقابلها،[٣] وللخط المتوسط عدّة خصائص منها ما يأتي:[٤]
- يُنصّف المتوسط زاوية الرأس المحصورة بين ضلعين متساويين إلى زاويتين متساويتين تماماً في كلٍّ من المثلث متساوي الساقين والمثلث متساوي الأضلاع.
- يمتلك المثلث 3 خطوط متوسطة تتقاطع في نقطة تُسمّى بالنقطة المركزيّة (بالإنجليزية: Centroid)، تقسم كل خطّ متوسط من الخطوط المتوسطة الثلاث بنسبة 2:1.
- يُنصّف كل متوسط المثلث إلى مثلثين متساويين بالمساحة.
- يُمكن حساب طول المتوسط عن طريق نظرية أبولونيوس:
- م أ=((2بَ²+2جَ²-أَ²)÷4)√، أو م ب=((2أَ²+2جَ²-بَ²)÷4)√، أو م ج=((2بَ²+2أَ²-جَ²)÷4)√؛ حيث:
- م أ: طول خط المتوسط النازل من الرأس أ، أَ: طول الضلع المقابل للرأس أ.
- م ب: طول خط المتوسط النازل من الرأس ب، بَ: طول الضلع المقابل للرأس ب.
- م ج: طول خط المتوسط النازل من الرأس ج، جَ: طول الضلع المقابل للرأس ج.
خصائص ارتفاع المثلث
يُعرّف الارتفاع (بالإنجليزية: Altitude) على أّنه العمود الممتد من رأس المثلث إلى الضلع المقابل له، والذي يُسمّى بالقاعدة،[٥] وللارتفاع عدّة خصائص منها ما يأتي:[٦]
- ارتفاع المثلث قد يقع داخله أو خارجه.
- لكل مثلث 3 ارتفاعات محتملة، واحد ممتد من كل رأس.
- الارتفاع هو أقصر مسافة من الرأس إلى الضلع المقابل له في المثلث.
- تلتقي الارتفاعات الثلاثة دائماً في نقطة واحدة بغض النظر عن شكل المثلث تُسمّى بملتقى الارتفاعات (بالإنجليزية: Ortho-centre of the triangle).
خصائص المثلث قائم الزاوية
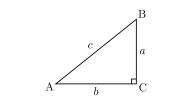
يُمكن تعريف المثلث قائم الزاوية (بالإنجليزية: Right-angle triangle) على أنه المثلث الذي يمتلك زاوية قائمة قياسها 90 درجة، وتكون باقي زواياه حادّة، ويُسمّى الضلع المقابل للزاوية القائمة بالوتر (بالإنجليزية: Hypotenuse) وهو أطول ضلع من أضلاع المثلث، ويُمكن حساب طوله باستخدام نظرية فيثاغورس، حيث يساوي مربع طول الوتر مجموع مربع كل ضلع من أضلاع المثلث الأخرى: (الوتر)²=(الضلع الأول)²+ (الضلع الثاني)²، وبالرموز: أ²=ب²+ج²؛ حيث:[١]
- أ: طول وتر المثلث قائم الزاوية.
- ب، ج: أطوال أضلاع المثلث قائم الزاوية الأخرى.
وللمثلث قائم الزاوية عدّة خصائص يُمكن تلخيصها على النحو الآتي:[٧]
- يُمكن أن يكون المثلث قائم الزاوية متساوي الساقين إذا تساوى طول الضلعين اللذين يحصران الزاوية القائمة بينهما.
- لا يُمكن للمثلث قائم الزاوية أن يكون متساوي الأضلاع؛ لأن طول الوتر دائماً أكبر من أطوال الأضلاع الأخرى.
- يُنصّف المتوسط الممتد من الوتر المثلث قائم الزاوية إلى مثلثين متطابقين يكون كلّ منها متساوي الساقين.[٨]
- يكون طول المتوسط المرسوم من الزاوية القائمة مساوياً لطول نصف الوتر.[٨]
- يملك المثلث قائم الزاوية ومتساوي الساقين زاوية قائمة وزاويتين حادّتين قياس كلّ منهما 45 درجة، ويكون طول الضلعين الآخرين فيه متساوياً.[٨]
- يمنلك المثلث قائم الزاوية ومختلف الأضلاع زاوية قائمة وزاويتين حادّتين قياس كلّ منهما مختلف عن الآخر، وتكون أطوال الأضلاع مختلفة أيضاً.[٨]
لمزيد من المعلومات حول المثلث قائم الزاوية يُمكنك قراءة المقالات الآتية: قانون المثلث قائم الزاوية، قانون مساحة المثلث قائم الزاوية، كيفية حساب محيط المثلث القائم، كيفية حساب أضلاع المثلث القائم.
خصائص المثلث متساوي الأضلاع
يُمكن تعريف المثلث متساوي الأضلاع (بالإنجليزية: Equilateral triangle) على أنه المثلث الذي تكون أضلاعه الثلاثة متساوية في الطول، وبالتالي ينتج أن جميع زواياه الداخليّة أيضاً متساوية في القياس، ويبلغ قياس كلّ منها 60 درجة،[١] وللمثلث متساوي الأضلاع عدّة خصائص يُمكن تلخيصها على النحو الآتي:[٩]
- يكون كلّ من الارتفاع، وخط المتوسط، ومُنصّف الزاوية، والمُنصّف العمودي لكل ضلع من الأضلاع وزاوية من الزوايا هو الخط نفسه، ويكون طولها متساوياً لجميع الأضلاع، ويساوي: (3√×س)÷2؛ حيث س: طول ضلع المثلث متساوي الأضلاع، وعليه تكون أطوال خط المتوسط الثلاثة في المثلث متساوي الأضلاع دائماً متساوية.[٤]
لمزيد من المعلومات حول المثلث متساوي الأضلاع يُمكنك قراءة المقالات الآتية: قانون مساحة المثلث متساوي الأضلاع.
خصائص المثلث متساوي الساقين
يُمكن تعريف المثلث متساوي الساقين (بالإنجليزية: Isosceles triangle) على أنه مثلث يتساوى طول ضلعين من أضلاعه، ويختلف الضلع الثالث في الطول عنهما، ويكون قياس الزاويتين المقابلتين للأضلاع المتساوية في الطول متساوياً في القياس (زوايا القاعدة)،[١] وللمثلث متساوي الساقين عدّة خصائص يُمكن تلخيصها على النحو الآتي:[١٠]
- تكون قاعدة المثلث متساوي الساقين هي الضلع الثالث الذي لا يساوي طوله طول الضلعيين الآخرين.
- يُنصّف الارتفاع المُمتد من رأس المثلث متساوي الساقين القاعدة إلى قسمين متساويين، و يُنصّف زاوية الرأس إلى قسمين متساويين أيضاً.
- يُنصّف الارتفاع المُمتد من رأس المثلث متساوي الساقين المثلث إلى مثلثين متطابقين قائمي الزاوية.
- الارتفاع في المثلث متساوي الساقين هو نفسه الخط المتوسط.[١١]
- يتساوى طول خطوط المتوسط المرسومة من الزوايا المتساوية في المثلث متساوي الساقين.[٤]
لمزيد من المعلومات حول المثلث متساوي الساقين يُمكنك قراءة المقالات الآتية: خصائص المثلث متساوي الساقين، قانون محيط المثلث متساوي الساقين، قانون مساحة المثلث متساوي الساقين.
خصائص المثلث مختلف الأضلاع
يُمكن تعريف المثلث مختلف الأضلاع (بالإننجليزية: Scalene triangle) على أنه مثلث تختلف أطوال أضلاعه الثلاثة وقياس زواياه عن بعضها البعض، وللمثلث مختلف عدّة خصائص يُمكن تلخيصها على النحو الآتي:[١٢]
- لا يمتلك المثلث مختلف الأضلاع أضلاعاً متساويةً في الطول.
- لا يمتلك المثلث مختلف الأضلاع زوايا متساوية في القياس.
- يُمكن أن تكون زوايا المثلث مختلف الأضلاع حادّة، أو منفرجة، أو قائمة.
- لا يمتلك المثلث مختلف الأضلاع خط تناظر.
- لا يمتلك المثلث مختلف الأضلاع نقطة تماثل.
- تكون أطوال خط المتوسط الثلاثة في المثلث مختلف الأضلاع دائماً مختلفة.[٤]
أمثلة متنوعة على خصائص المثلث
- المثال الأول: إذا كان المثلث أب ج مثلث قائم الزاوية في ج، وكانت د نقطة على الوتر أب، وكان ج د يُعامد أب، وقياس الزاوية دأج=°65، فما هو قياس كلّ من الزاويا: أج د، أب ج؟[١٣]الحل:
- مجموع زوايا المثلث ∆أج د=180، ومنه ∠أد ج+∠دأج+∠أج د=180، 90+65+∠أج د=180، ومنه ∠أج د=°25.
- بما أن أج يُعامد أج فإن الزاوية أج ب=90 درجة، وهي تساوي ∠ب ج د+∠أج د، ومنه: ∠ب ج د+∠25=90، ومنه ∠ب ج د=°65.
- مجموع زوايا المثلث ∆ب دج=180، ومنه ∠ج ب د+∠ب دج+∠ ب ج د=180، ∠ج ب د+90+65=180، ومنه ∠ج ب د=°25، والزاويتان ∠أب ج=∠ج ب د=°25.
- المثال الثاني: إذا كان المثلث أب ج مثلث متساوي الساقين حيث أب=أج، وكان قياس الزاوية أ=100°، ما هو قياس الزاوية ج؟[١]الحل:
- بما أن المثلث أب ج مثلث متساوي الساقين فقياس الزاويتين ⦣ب=⦣ ج.
- مجموع زوايا المثلث ∆أب ج=180، ومنه ∠أ+∠ب+∠ج=180، 100+⦣ ج+⦣ ج =180، ومنه 100+2×⦣ ج=180، ومنه ⦣ ج=(180-100)÷2، ومنه ⦣ ج=°40.
- وبما ان ⦣ب=⦣ ج بالتالي قياس ⦣ب=°40.
- المثال الثالث: هل من الممكن أن يكون هناك مثلث أطوال أضلاعه هي: 5 سم، 6 سم، 4 سم؟[١٤]الحل:
- إذا كان مجموع أطوال أي ضلعين أكبر من الضلع الثالث، فإن هذه الأضلاع تشكّل مثلثاً، وعليه: 5+6>4، 5+4>6، 4+6>5، إذن يُمكن أن لهذه الأضلاع أن تشكّل مثلثاً.
- المثال الرابع: تم تقصير أطوال أضلاع مثلث متساوي الأضلاع ليقل كل ضلع منها في طوله: 12سم، 13سم، 14سم، على الترتيب، وعليه أصبح هذا المثلث قائم الزاوية، جد طول كل ضلع من الأضلاع قبل تقصيرها؟[١٥]الحل:
- نفترض أن س هو طول الأضلاع قبل تقصيرها، وعليه يكون طول أضلاع المثلث الأصلي بعد التقصير: (س-12)، (س-13)، (س-14).
- بما أنه تشكّل لدينا مثلث قائم الزاوية بعد تقصير الأضلاع، فإنه وبعد افتراض أن الضلع (س-12) هو الوتر؛ لأنه أطول الأضلاع، يمكن التعويض في نظريّة فيثاغورس لينتج أن: أ²=ب²+ج²، (س-12)²= (س-14)²+(س-13)²، ومنه س²-24س+144= (س²-28س+196)+( س²-26س+169)، وبجمع الحدود المتشابهة ينتج أن: س²-30س+221، ومنه ينتج (س-13)(س-17)=0، وعليه قيمة س=17؛ لأنه لا يُمكن لاحد الأضلاع أن يكون سالباً، وذلك عند تعويض القيم فيما بعد.
- تعويض قيمة (س) للحصول على أطوال الأضلاع لينتج أن:
- س-12= 17-12 = 5سم.
- س-13 = 17-13 =4سم.
- س-14= 17-14 = 3سم.
- المثال الخامس: هل يُمكن أن لزوايا مثلث أن يكون قياسها 90°، 60°، 30°؟[١٥]الحل:
- يجب أن يكون مجموع زوايا المثلث=180، فبجمع زوايا المثلث 90+60+30 ينتج أن مجموعها يساوي 180°، بالتالي يُمكن للمثلث أن يمتلك هذه الزوايا.
- المثال السادس: مثلث زاويته الثانية أكبر بمقدار 5 درجات من الزاوية الأولى، والزاوية الثالثة أكبر بمقدار 5 درجات من الزاوية الثانية ما هو قياس الزوايا الثلاث؟[١٥]الحل:
- نفرض أن قياس الزاوية الأولى=س، وقياس الزاوية الثانية=س+5، وقياس الزاوية الثالثة=5+(س+5)=س+10.
- مجموع زوايا المثلث =180، وبالتالي: س+(س+5)+(س+10)=180، ومنه 3س+15=180، وبالتالي س=(180-15)÷3، فينتج أن قياس الزاوية الأولى س=55.
- تعويض قيمة س لإيجاد قياس باقي الزوايا، قياس الزاوية الثانية=س+5=55+5=60، وقياس الزاوية الثالثة= س+10=55+10=65، بالتالي ينتج أن قياس الزوايا هو: (55°، 60°، 65°).
- المثال السابع: إذا كان قياس زوايا مثلث هي ثلاثة اعداد صحيحة موجبة متتالية، ما هو قياس هذه الزوايا؟[١٦]الحل:
- نفرض أن قياس الزاوية الأولى=س، وقياس الزاوية الثانية=س+1، وقياس الزاوية الثالثة=س+2.
- مجموع زوايا المثلث =180، وعليه: س+(س+1)+(س+2)=180، ومنه: 3س+3=180، بالتالي س=(180-3)÷3، فينتج أن قياس الزاوية الأولى س=59.
- تعويض قيمة س لإيجاد قياس باقي الزوايا، قياس الزاوية الثانية=س+1=59+1=60، وقياس الزاوية الثالثة=س+2=59+2=61، بالتالي ينتج أن قياس الزوايا هو: (59°، 60°، 61°).
- المثال الثامن: مثلث قائم الزاوية قياس زواياه غير القائمتين هو: س+1، 2س+5، ما هو قياس هذه الزوايا بالدرجات؟[١٧]الحل:
- مجموع زوايا المثلث =180، وعليه: 90+(س+1)+(2س+5)=180، ومنه 3س+96=180، وبالتالي س=(180-96)÷3، فينتج أن قيمة س=28.
- تعويض قيمة س لإيجاد قياس الزوايا، وعليه قياس الزاوية الثانية=س+1=28+1=29، وقياس الزاوية الثالثة=2س+5=(2×28)+5=61، وبالتالي ينتج أن قياس الزوايا الأخرى هو: (29°، 61°).
المراجع
- ^ أ ب ت ث ج ح خ Asif M (25-7-2019), "Properties of triangle – Important formulas and classification"، www.e-gmat.com, Retrieved 23-4-2020. Edited.
- ↑ "Properties of Triangle", www.byjus.com, Retrieved 23-4-2020. Edited.
- ↑ "Median of Triangle", www.mathsisfun.com, Retrieved 23-4-2020. Edited.
- ^ أ ب ت ث Kasia Mikoluk, "Median of Triangle: Definition and Essential Properties"، www.udemy.com, Retrieved 23-4-2020. Edited.
- ↑ "Triangles: Theory and Formulas", www.hitbullseye.com, Retrieved 23-4-2020. Edited.
- ↑ "Altitude And Median Of A Triangle", www.byjus.com, Retrieved 23-4-2020. Edited.
- ↑ "Right Triangle", www.mathopenref.com, Retrieved 23-4-2020. Edited.
- ^ أ ب ت ث Gabriela Briceño V, "Right triangle"، www.euston96.com, Retrieved 23-4-2020. Edited.
- ↑ [ https://brilliant.org/wiki/properties-of-equilateral-triangles/ "Properties of Equilateral Triangles"], www.brilliant.org, Retrieved 23-4-2020. Edited.
- ↑ "Properties of Isosceles Triangle", www.byjus.com, Retrieved 23-4-2020. Edited.
- ↑ Niranjan Khanderia, Archit Boobna, Alexander Katz, and 8 others, "Properties of Isosceles Triangles"، www.brilliant.org, Retrieved 23-4-2020. Edited.
- ↑ "Scalene Triangle", www.byjus.com, Retrieved 23-4-2020. Edited.
- ↑ MBA Crystal Ball (16-10-2015), "Triangles properties and types | GMAT GRE Geometry Tutorial"، www.mbacrystalball.com, Retrieved 23-4-2020. Edited.
- ↑ "PROPERTIES OF TRIANGLE", www.onlinemath4all.com, Retrieved 23-4-2020. Edited.
- ^ أ ب ت "properties of triangle", www.onlinemath4all.com, Retrieved 23-4-2020. Edited.
- ↑ "PROPERTIES OF TRIANGLE", www.onlinemath4all.com, Retrieved 23-4-2020. Edited.
- ↑ "properties of triangle", www.onlinemath4all.com, Retrieved 23-4-2020. Edited.