محتويات

نص قانون نظرية فيثاغورس
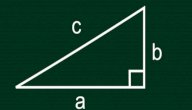
تنصّ نظرية فيثاغورس على أنّ: "'مجموع مربعي طولي ضلعي القائمة، وهما الضلعين الأقصر في المثلث قائم الزاوية مساوٍ لمربع طول الوتر وهو الضلع الأطول في المثلث'"، [١] وبالرموز: نظريّة فيثاغورس= أ²+ ب²=ج²؛ حيث:[٢]
- أ، ب: ضلعا المثلث القائم أب ج.
- ج: وتر المثلث القائم أب ج، وهو الضلع الأطول فيه.
ويجدر بالذكر هنا أن معكوس النظريّة أيضاً صحيح؛ حيث إن المثلث الذي تنطبق عليه نظريّة فيثاغورس، وهي: أ²+ ب²=ج²، هو بالضرورة مثلث قائم الزاوية.[٣]
لمزيد من المعلومات والأمثلة حول المثلثات يُمكنك قراءة المقالات الآتية: كيف أحسب ارتفاع المثلث، حساب زوايا المثلث، قانون محيط المثلث، كيف أحسب مساحة المثلث، انواع المثلثات، بحث رياضيات عن المثلثات.
إثبات نظرية فيثاغورس
يُمكن إثبات نظرية فيثاغورس بعدد لا نهائي من البراهين، وقد نشر عالم الرياضيات إليشا سكوت لوميس (بالإنجليزية: Elisha Scott Loomis) كتابه "فرضيّة فيثاغورس" عام 1927م، والذي قدّم فيه 370 برهاناً مختلفاً للنظريّة صُنّفت في أربعة أقسام رئيسة هي: قسم الجبر الذي يربط جوانب المثلث، وقسم الهندسة الذي يقارن بين المساحات، وقسم الحركية أو الديناميكيّة الذي يرتبط بخصائص القوة والكتلة، وأخيراً المتجهات.[٤]
ويُمكن إثبات نظريّة فيثاغورس هندسياّ كما يأتي:[٥]
- افتراض أن هناك مربعاً تقع النقاط (د، هـ، و، ي) على أضلاعه الأربعة، بحيث تقسم كل نقطة منها الضلع إلى قسمين طول أحدهما هو: أ، والقسم الثاني هو: ب، ثم تم الوصل بين هذه النقاط بخطوط مستقيمة ليتكوّن مربع داخلي طول ضلعه هو (جـ)، وأربعة مثلثات داخلية قائمة الزاوية وترها هو (جـ)، وطول ضلعيها الآخرين هما: (أ،ب)، لينتج أن طول الضلع للمربع الخارجي هو (أ+ب).
- التعبير عن مساحة المربع الخارجي بالقيمة: (أ+ب)²، وهي تساوي مساحة المثلثات الأربع الداخلية: 4×(½× طول القاعدة× الارتفاع)= 4/2×أ×ب=2أب، إضافةً إلى مساحة المربع الداخلي: جـ²، وبالتالي ينتج أن مساحة المربع الخارجي بالرموز هي: (أ+ب)²= 2أب+ ج²، وبفك التربيع ينتج: أ²+2أب +ب²= 2أب+ ج²، ثمّ بترتيب طرفي المعادلة ينتج أن: أ²+ب²= 2أب+ ج²-2أب ، ثم باختصار الحدود ينتج أن: أ² + ب² = ج²، وبما أن ج هو الوتر، ينتج أن مربع الوتر يساوي مجموع مربعي الضلعين وهذا ما نصّت عليه نظرية فيثاغورس.
لمزيد من المعلومات والأمثلة حول المثلث قائم الزاوية يُمكن قراءة المقالات الآتية: قانون المثلث قائم الزاوية، كيفية حساب محيط المثلث القائم، ارتفاع المثلث القائم.
أمثلة متنوعة حول نظرية فيثاغورس
- المثال الأول: مثلث قائم الزاوية طول ضلعه الأول 12سم والثاني 5سم، ما هو طول وتره؟[١]
- الحل:
- تعويض قيمة أطوال الأضلاع في معادلة فيثاغورس: أ²+ ب²= ج²، لينتج أن: (12)²+(5)²= ج²، لينتج أن ج²= 169، وبأخذ الجذر التربيعي للطرفين ينتج أن ج=13، ومنه طول الوتر=13سم.
- المثال الثاني: ما هو قطر مربع مساحته 1سم؟[٢]
- الحل:
- قطر المربع يقسمه إلى مثلثين متطابقين وقائمي الزاوية، كما أن أطوال أضلاع المربع= أطوال أضلاع المثلث قائم الزاوية=1سم.
- تعويض قيمة أطوال الأضلاع في معادلة فيثاغورس، لينتج أن: أ²+ ب²= ج²، (1)²+(1)²= ج²، لينتج أن ج²= 2، وبأخذ الجذر التربيعي للطرفين ينتج أن ج=1.414، ومنه طول الوتر= طول قطر المربع=1.414سم.
- المثال الثالث: مثلث أطوال أضلاعه هي 26سم، 10سم، 24سم، هل هو قائم الزاوية؟[٢]
- الحل:
- تعويض قيمة أطوال الأضلاع في معادلة فيثاغورس: أ²+ ب²= ج²، (10)²+(24)²= (26)²، ثم حساب قيمة الطرف الأيمن: 100+ 576= 676، وحساب قيمة الطرف الأيسر: وهو (26)²=676، وعليه 676=676 وبما أنّ طرفي المعادلة متساويان فبالتالي المثلث قائم الزاوية.
- المثال الرابع: مثلث أطوال أضلاعه هي 9، 6، 7، هل هو قائم الزاوية؟[١]
- الحل:
- تعويض قيمة أطوال الأضلاع في معادلة فيثاغورس: أ²+ ب²= ج²، لينتج أن: (6)²+(7)²= (9)²، ثم حساب قيمة الطرف الأيمن: 36+ 49=85، وحساب قيمة الطرف الأيسر: (9)²=81، ومنه 85≠81 وبما أنّ طرفي المعادلة غير متساويين فبالتالي المثلث ليس قائم الزاوية.
- المثال الخامس: سُلّم بطول 15م يصل إلى نافذة بارتفاع 9م عن سطح الأرض على أحد جانبي الشارع، وعند قلب السلم إلى الاتجاه الآخر مع إبقاء قاعدته في نفس النقطة فإنه يصل إلى نافذة أخرى بارتفاع 12م عن سطح الأرض في الجانب الآخر من الشارع، ما هو عرض الشارع؟[٦]
- الحل:
- نفرض أن السلم يُشكّل مع كلّ من النافذتين مثلثين قائمين، الأول أب ج قائم في ب، والثاني دهـ ج قائم في هـ، ويلتقيان في النقطة ج وهي النقطة التي يرتكز عليها السلم.
- تعويض قيمة طول كل من الضلع والوتر في معادلة فيثاغورس للمثلث الأول: (أب)² + (ب ج)² = (أج)²، (9)²+ (ب ج)² = (15)²، لينتج أن (ب ج)² = 225-81=144، وبأخذ الجذر التربيعي للطرفين ينتج أن ب ج =12م، وهو القسم الأول من الشارع.
- تعويض قيمة طول كل من الضلع والوتر في معادلة فيثاغورس للمثلث الثاني: (دهـ)² + (هـ ج)² = (دج)²، (12)²+ (هـ ج)² = (15)²، لينتج أن (هـ ج)² = 225-144=81، وبأخذ الجذر التربيعي للطرفين ينتج أن هـ ج =9م، وهو القسم الثاني للشارع.
- حساب عرض الشارع (هـ ب) بجمع القسمين: ب ج+ هـ ج = 12+ 9= 21م.
- المثال السادس: إذا كان طول الوتر في مثلث قائم الزاوية هو 13سم، وطول أحد الأضلاع هو 5سم، فما هو طول الضلع الآخر؟[٧]
- الحل:
- تعويض قيمة طول كل من الضلع والوتر في معادلة فيثاغورس: أ²+ ب²= ج²، لينتج أنّ: (5)²+ ب²= (13)²، لينتج أن: ب²=169-25=144، وبأخذ الجذر التربيعي للطرفين ينتج أن ب =12سم.
نظرة عامة حول قانون نظرية فيثاغورس
تُعتبر نظريّة فيثاغورس (بالإنجليزية: Pythagorean Theorem) واحدة من أقدم النظريات المعروفة للحضارات القديمة، وقد تمت تسميتها نسبة إلى عالم الرياضيات والفيلسوف اليونانيّ فيثاغورس، وتُعدّ النظريّة أشهر مساهماته في علم الرياضيات، ويرجع الفضل إليه في العديد من المساهمات الأخرى في الرياضيات والتي قد يكون بعضها من عمل طلابه، كما أسّس العالم فيثاغورس مدرسته للرياضيات في منطقة كورتونا التي كانت ميناءً يونانياً جنوب إيطاليا،[٤] وتُستخدم نظرية فيثاغورس بشكل عملي في مجموعة واسعة من المجالات المختلفة مثل:[٨]
- البناء: ويمثّل ذلك في وضع أُسس المباني، فإنشاء أساس ذي شكل مستطيل لأي مبنى يتطلّب إنشاء زوايا قائمة، وبما أن الطول والعرض موجودان فبالتالي يُمكن استخدام نظرية فيثاغورس لحساب وعمل الزوايا القائمة بشكل صحيح ودقيق.
- الملاحة: ويتمثّل ذلك في نظام القياس الذي يسمح للطيارين بالتنقل في الأجواء العاصفة، ويسمح للسفن بتحديد المسار وحساب المسافة إلى نقطة معيّنة في المحيط، كما أنه مفيد لرسامي الخرائط الذين يستخدمونه لحساب انحدار التلال والجبال، وتُعتبر النظرية هي الأساس في جميع قياسات نظام التموضع العالمي (بالإنجليزية: GPS).
- الهندسة وعلوم الرياضيات والصناعة: تُعتبرالنظرية أساسية في الفروع الأخرى للرياضيات مثل الهندسة الفراغيّة، إضافةً إلى الفيزياء، وعلوم الأرض، والهندسة الميكانيكية وهندسة الطيران، كما يستخدمها النجارون والميكانيكيون.
المراجع
- ^ أ ب ت Nick Lee, Sharky Kesa, Niranjan Khanderia, and 16 others, "Pythagorean Theorem"، www.brilliant.org, Retrieved 31-3-2020. Edited.
- ^ أ ب ت "Pythagoras' Theorem", www.mathsisfun.com, Retrieved 31-3-2020. Edited.
- ↑ Anthony Powell, "Pythagorean Theorem"، www.cut-the-knot.org, Retrieved 31-3-2020. Edited.
- ^ أ ب Stephanie J. Morris, "The Pythagorean Theorem"، www.jwilson.coe.uga.edu, Retrieved 31-3-2020. Edited.
- ↑ "Pythagorean theorem", www.sangakoo.com, Retrieved 31-3-2020. Edited.
- ↑ "pythagorean theorem formula", www.vedantu.com, Retrieved 31-3-2020. Edited.
- ↑ "Pythagorean Theorem Formula", www.byjus.com, Retrieved 31-3-2020. Edited.
- ↑ PATRICK J. KIGER (8-11-2019), "The Pythagorean Theorem Makes Construction and GPS Possible"، www.science.howstuffworks.com, Retrieved 31-3-2020. Edited.